题目内容
已知a-b=5，且c-b=10，则a2+b2+c2-ab-bc-ac等于
- A.105
- B.100
- C.75
- D.50
C
分析：由已知a-b=5，且c-b=10，两等式左右两边分别相减，可得到a-c=-5，观察a2+b2+c2-ab-bc-ac发现，利用完全平方差公式，可转化为
[（a-b）2+（b-c）2+（a-c）2]，再将上面的式子代入，问题得解．
解答：∵a-b=5，c-b=10
∴a-c=-5
a2+b2+c2-ab-bc-ac=[（a-b）2+（b-c）2+（a-c）2]=×[52+（-10）2+（-5）2]=75
故答案为C
点评：本题主要考查完全平方差公式因式分解．将a2+b2+c2-ab-bc-ac看做[（a-b）2+（b-c）2+（a-c）2]是难点．
分析：由已知a-b=5，且c-b=10，两等式左右两边分别相减，可得到a-c=-5，观察a2+b2+c2-ab-bc-ac发现，利用完全平方差公式，可转化为
[（a-b）2+（b-c）2+（a-c）2]，再将上面的式子代入，问题得解．解答：∵a-b=5，c-b=10
∴a-c=-5
a2+b2+c2-ab-bc-ac=
[（a-b）2+（b-c）2+（a-c）2]=×[52+（-10）2+（-5）2]=75故答案为C
点评：本题主要考查完全平方差公式因式分解．将a2+b2+c2-ab-bc-ac看做
[（a-b）2+（b-c）2+（a-c）2]是难点． 
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
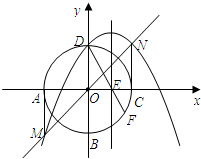C、D四点．过点A和点C分别作⊙O的切线MA、NC，它们分别与直线y=x交于点M、N，
已知直线l1∥l2，且 l3、l4和l1、l2分别交于A、B、C、D四点，点P在直线AB上运动．设∠ADP=∠1，∠DPC=∠2，∠BCP=∠3．