题目内容
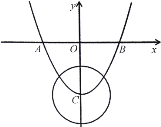
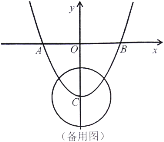
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 的半径为
的半径为![]() ,
,![]() 为
为![]() 上一动点.
上一动点.
(1)求点![]() ,
,![]() 的坐标?
的坐标?
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ,或
,或 或
或 ;
;
【解析】
(1)在抛物线解析式中令y=0可求得B点坐标,令x=0可求得C点坐标;
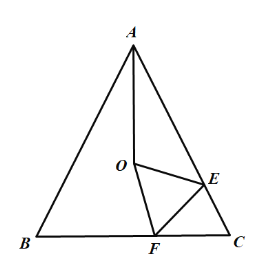
(2)①当PB与⊙相切时,△PBC为直角三角形,根据勾股定理得到BC=5,![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,易得
,易得![]() ,四边形
,四边形![]() 是矩形,根据相似三角形的性质得到
是矩形,根据相似三角形的性质得到![]() ,设
,设![]() ,
,![]() ,得到BE=3x,CF=2x4,于是得到
,得到BE=3x,CF=2x4,于是得到![]() ,
,![]() ,求得
,求得![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,同理求得
,同理求得![]() ;②当BC⊥PC时,△PBC为直角三角形,过
;②当BC⊥PC时,△PBC为直角三角形,过![]() 作
作![]() 轴于
轴于![]() ,易得
,易得![]() ,根据相似三角形的性质求出
,根据相似三角形的性质求出![]() ,
,![]() 即可得到
即可得到![]() ,同理可得
,同理可得![]() .
.
即可得到结论;
(1)在![]() 中,令
中,令![]() ,解得:
,解得:![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ;
;
(2)存在点![]() ,使得
,使得![]() 为直角三角形,
为直角三角形,
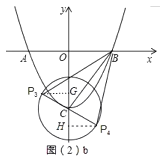
①当![]() 与
与![]() 相切时,
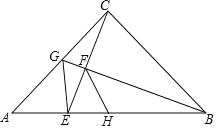
相切时,![]() 为直角三角形,如图(2)
为直角三角形,如图(2)![]() ,连接
,连接![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,易得
,易得![]() ,四边形
,四边形![]() 是矩形,
是矩形,

∴![]() ,
,
设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,同理求得
,同理求得![]() ;
;
②当![]() 时,
时,![]() 为直角三角形,过
为直角三角形,过![]() 作
作![]() 轴于
轴于![]() ,如图(2)
,如图(2)![]() ,易得
,易得![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴ ;
;
同理可得: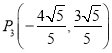 ;
;
综上所述:点![]() 的坐标为:
的坐标为:![]() 或
或![]() ,或
,或 或
或 .
.

练习册系列答案
相关题目