Question

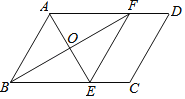
【题目】如图，点E为△ABC的内心，过点E作MN∥BC交AB于点M，交AC于点N，若AB＝7，AC＝5，BC＝6，则MN的长为（　　）

A. 3.5B. 4C. 5D. 5.5

Answer 1

【答案】B

【解析】

连接EB、EC，如图，利用三角形内心的性质得到∠1＝∠2，利用平行线的性质得∠2＝∠3，所以∠1＝∠3，则BM＝ME，同理可得NC＝NE，接着证明△AMN∽△ABC，所以＝，则BM＝7﹣MN①，同理可得CN＝5﹣MN②，把两式相加得到MN的方程，然后解方程即可．

解：连接EB、EC，如图，

∵点E为△ABC的内心，

∴EB平分∠ABC，EC平分∠ACB，

∴∠1＝∠2，

∵MN∥BC，

∴∠2＝∠3，

∴∠1＝∠3，

∴BM＝ME，

同理可得NC＝NE，

∵MN∥BC，

∴△AMN∽△ABC，

∴，即，则BM＝7﹣MN①，

同理可得CN＝5﹣MN②，

①+②得MN＝12﹣2MN，

∴MN＝4．

故选：B．