题目内容
如图，小明同学在东西走向的文一路A处，测得一处公共自行车租用服务点P在北偏东60°方向上，在A处往东90米的B处，又测得该服务点P在北偏东30°方向上，则该服务点P到文一路的距离PC为（ ）A、60
| ||
B、45
| ||
C、30
| ||
| D、45米 |
分析：分别在两个直角三角形中由锐角三角函数的定义用PC分别表示出AC、BC，利用两线段的差等于90列出关于线段PC的式子，求得PC即可．
解答：解：∵在Rt△PBC中，
=tan∠PBC，
∴BC=
=
PC，
∵在Rt△PAC中，
=tan∠PAC，
∴AC=
=
PC，
∵AB=AC-BC=90，
∴
PC-
PC=90，
解得：PC=45
．
故选B．
| PC |
| BC |
∴BC=
| PC |
| tan60° |
| ||
| 3 |
∵在Rt△PAC中，
| PC |
| AC |
∴AC=
| PC |
| tan30° |
| 3 |
∵AB=AC-BC=90，
∴
| 3 |
| ||
| 3 |
解得：PC=45
| 3 |
故选B．
点评：本题考查了解直角三角形的知识，解决此题的关键是弄清直角三角形的三边与其锐角的关系，进而列出有关的等式，解之即可．
练习册系列答案
相关题目
如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC=
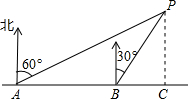如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC=（ ）米．| A、250 | ||
| B、500 | ||
C、250
| ||
D、500
|
如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处正东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC等于多少米？