题目内容
△ABC中，AC=5，中线AD=7，则AB边的取值范围是
- A.1＜AB＜29
- B.4＜AB＜24
- C.5＜AB＜19
- D.9＜AB＜19
D
分析：延长AD至E，使DE=AD，连接CE，使得△ABD≌△ECD，则将AB和已知线段转化到一个三角形中，进而利用三角形的三边关系确定AB的范围即可．
解答：
解：延长AD至E，使DE=AD，连接CE．
在△ABD和△ECD中，BD=CD，∠ADB=∠EDC，AD=ED，
∴△ABD≌△ECD（SAS）．
∴AB=CE．
在△ACE中，根据三角形的三边关系，得
AE-AC＜CE＜AE+AC，
即9＜CE＜19．
则9＜AB＜19．
故选D．
点评：解决此题的关键是通过倍长中线，构造全等三角形，把要求的线段和已知的线段放到一个三角形中，再根据三角形的三边关系进行计算．
分析：延长AD至E，使DE=AD，连接CE，使得△ABD≌△ECD，则将AB和已知线段转化到一个三角形中，进而利用三角形的三边关系确定AB的范围即可．
解答：
解：延长AD至E，使DE=AD，连接CE．在△ABD和△ECD中，BD=CD，∠ADB=∠EDC，AD=ED，
∴△ABD≌△ECD（SAS）．
∴AB=CE．
在△ACE中，根据三角形的三边关系，得
AE-AC＜CE＜AE+AC，
即9＜CE＜19．
则9＜AB＜19．
故选D．
点评：解决此题的关键是通过倍长中线，构造全等三角形，把要求的线段和已知的线段放到一个三角形中，再根据三角形的三边关系进行计算．
练习册系列答案
相关题目
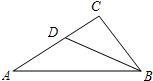如图，在△ABC中，AC＞BC，D是AC边上一点，连接BD．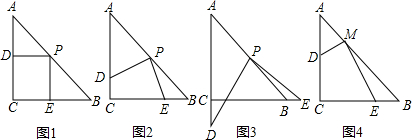
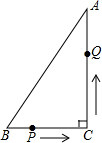如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．