题目内容
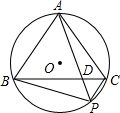
 已知:如图,在⊙O的内接等边三角形ABC中,经过点A的弦与BC和弧
已知:如图,在⊙O的内接等边三角形ABC中,经过点A的弦与BC和弧 分别相交于点D和P,连接PB、PC.
分别相交于点D和P,连接PB、PC.
(1)写出图中所有的相似三角形:______;
(2)求证:PA2=BC2+PB•PC.
 (1)解:△ADB∽△CDP,△ADC∽△BDP,△ABD∽△APB,
(1)解:△ADB∽△CDP,△ADC∽△BDP,△ABD∽△APB,△ADC∽△ACP,△BDP∽△ACP,△APB∽△CPD;
(2)证明:∵△ADC∽△BDP
∴

∴AD=

∵△ADB∽△CDP
∴

∴PD=

∴PA=AD+PD=
 +
+ =
=
∴

∵∠ABD=∠ACB=∠APB=60°
∵∠BAP=∠DAB
∴△ABD∽△APB
∴

即PA=

∴PA2=BC2+PB•PC
分析:(1)利用同弧所对的圆周角相等,证得角相等,即可证得相似三角形;
(2)利用相似三角形的性质求得即可.
点评:此题考查了圆的性质、相似三角形的判定与性质及比例变形.此题有一定难度,解题要细心.

练习册系列答案
相关题目
 已知:如图,在⊙O的内接等边三角形ABC中,经过点A的弦与BC和弧
已知:如图,在⊙O的内接等边三角形ABC中,经过点A的弦与BC和弧
 7、已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )
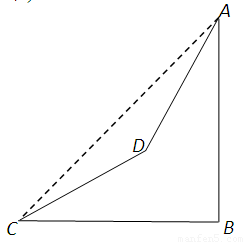
7、已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )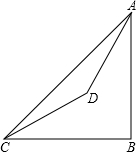 已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.
已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB. 处测得山顶
处测得山顶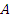 的仰角为
的仰角为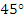 ,沿着坡角为
,沿着坡角为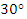 的斜坡前进
的斜坡前进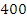 米到达
米到达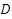 处(即∠
处(即∠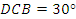 ,
, 米),测得
米),测得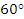 ,求山的高度
,求山的高度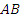 .
.