题目内容
如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为__________cm．
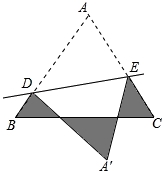
3cm．
【考点】翻折变换（折叠问题）；轴对称的性质．
【分析】由题意得AE=A′E，AD=A′D，故阴影部分的周长可以转化为三角形ABC的周长．
【解答】解：将△ADE沿直线DE折叠，点A落在点A′处，
所以AD=A′D，AE=A′E．
则阴影部分图形的周长等于BC+BD+CE+A′D+A′E，
=BC+BD+CE+AD+AE，
=BC+AB+AC，
=3cm．
故答案为：3．
【点评】折叠问题的实质是“轴对称”，解题关键是找出经轴对称变换所得的等量关系．
练习册系列答案
相关题目
某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：
| 类型 价格 | 进价（元/盏） | 售价（元/盏） |
| A型 | 30 | 45 |
| B型 | 50 | 70 |
（1）设商场购进A型节能台灯为x盏，销售完这批台灯时可获利为y元，求y关于x的函数解析式；
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
与△ABC关于x轴对称的图形△A1B1C1；
