题目内容
△ABC≌△AB′C′，其中∠A′=35°，∠B=70°，则∠C的度数为
- A.55°
- B.60°
- C.70°
- D.75°
D
分析：根据两三角形全等可得两个三角形的对应角相等，即∠A′=∠A，∠B=∠B′，∠C=∠C′，已知两角的度数，再根据三角形内角和度数即可得∠C的度数．
解答：∵△ABC≌△AB′C′，
∴∠A′=∠A，∠B=∠B′，∠C=∠C′，
已知∠A′=35°，∠B=70°，
∴∠C=180°-∠A-∠B=180°-35°-70°=75°．
故选D．
点评：本题考查了全等三角形的性质和三角形内角和定理，熟练掌握全等三角形的性质是解此题的关键．
分析：根据两三角形全等可得两个三角形的对应角相等，即∠A′=∠A，∠B=∠B′，∠C=∠C′，已知两角的度数，再根据三角形内角和度数即可得∠C的度数．
解答：∵△ABC≌△AB′C′，
∴∠A′=∠A，∠B=∠B′，∠C=∠C′，
已知∠A′=35°，∠B=70°，
∴∠C=180°-∠A-∠B=180°-35°-70°=75°．
故选D．
点评：本题考查了全等三角形的性质和三角形内角和定理，熟练掌握全等三角形的性质是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
（2005•乌兰察布）如图，已知AC平分∠PAQ，点B，B′分别在边AP，AQ上．下列条件中不能推出AB=AB′的是（ ）
如图，点C是∠PAQ的平分线上一点，点B、B′分别在边AP、AQ上，如果再添加一个条件，即可推出AB=AB′，那么该条件不可以是（ ）
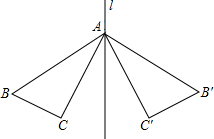如图，△ABC和△AB′C′关于直线l对称，下列结论：