题目内容
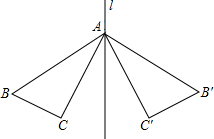如图，△ABC和△AB′C′关于直线l对称，下列结论：（1）∠ABC≌△AB′C′；
（2）∠BAC′=∠B′AC；
（3）l垂直平分CC′；
（4）直线BC和B′C′的交点不一定在l上．
其中正确的有（ ）
分析：根据成轴对称的两个图形能够完全重合可得△ABC和△AB′C′全等，然后对各小题分析判断后利用排除法求解．
解答：解：∵△ABC和△AB′C′关于直线L对称，
∴（1）△ABC≌△AB′C′，正确；
（2）∠B′AC=∠B′AC正确；
（3）直线L一定垂直平分线段C C′，故本小题正确；
（4）根据对应线段或其延长线的交点在对称轴上可知本小题正确；
综上所述，正确的结论有4个．
故选A．
∴（1）△ABC≌△AB′C′，正确；
（2）∠B′AC=∠B′AC正确；
（3）直线L一定垂直平分线段C C′，故本小题正确；
（4）根据对应线段或其延长线的交点在对称轴上可知本小题正确；
综上所述，正确的结论有4个．
故选A．
点评：本题考查了轴对称的性质，根据成轴对称的两个图形能够完全重合判断出两个三角形全等是解题的关键．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
10、如图，△ABC和△ADE都是等腰直角三角形，∠ACB和∠AED都是直角，点C在AD上，如果△ABC经旋转后能与△ADE重合，那么点
如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，BC=3，CD=1．
如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交 CE于点G，连接BE．下列结论中：
如图，△ABC和△ADE都是等腰直角三角形，AB=AC，AD=AE，∠BAC=∠DAE=90°．