题目内容
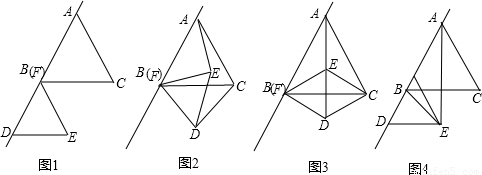
如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个 边长为1的小三角形,若 ,则△ABC的周长是 .
,则△ABC的周长是 .
【答案】分析:设正△ABC的边长为x,根据等边三角形的高为边长的 倍,求出正△ABC的面积,再根据菱形的性质结合图形表示出菱形的两对角线,然后根据菱形的面积等于两对角线乘积的一半表示出菱形的面积,然后根据所分成的小正三角形的个数的比等于面积的比列式计算即可得解.
倍,求出正△ABC的面积,再根据菱形的性质结合图形表示出菱形的两对角线,然后根据菱形的面积等于两对角线乘积的一半表示出菱形的面积,然后根据所分成的小正三角形的个数的比等于面积的比列式计算即可得解.
解答:解:设正△ABC的边长为x,则高位 x,
x,
S△ABC= x•
x• x=
x= x2,
x2,
∵所分成的三角形都是正三角形,
∴结合图形可得黑色菱形的较长的对角线的长是 x-
x- ,较短对角线的长为(
,较短对角线的长为( x-
x- )•
)• =
= x-1,
x-1,
∴黑色菱形的面积是 •(
•( x-
x- )•(
)•( x-1)=
x-1)= (x-2)2,
(x-2)2,
∴ =
= =
= ,
,
4x2-25x+25=0,
解得:x1= (因为分成边长为1的正三角形,所以此数不符合舍去),x2=5,
(因为分成边长为1的正三角形,所以此数不符合舍去),x2=5,
∴△ABC的周长是3×5=15,
故答案为:15.
点评:本题考查了菱形的性质,等边三角形的性质,熟练掌握有一个角等于60°的菱形的两条对角线的关系是解题的关键,本题难点在于根据三角形的面积与菱形的面积列出方程.
 倍,求出正△ABC的面积,再根据菱形的性质结合图形表示出菱形的两对角线,然后根据菱形的面积等于两对角线乘积的一半表示出菱形的面积,然后根据所分成的小正三角形的个数的比等于面积的比列式计算即可得解.
倍,求出正△ABC的面积,再根据菱形的性质结合图形表示出菱形的两对角线,然后根据菱形的面积等于两对角线乘积的一半表示出菱形的面积,然后根据所分成的小正三角形的个数的比等于面积的比列式计算即可得解.解答:解:设正△ABC的边长为x,则高位
 x,
x,S△ABC=
 x•
x• x=
x= x2,
x2,∵所分成的三角形都是正三角形,
∴结合图形可得黑色菱形的较长的对角线的长是
 x-
x- ,较短对角线的长为(
,较短对角线的长为( x-
x- )•
)• =
= x-1,
x-1,∴黑色菱形的面积是
 •(
•( x-
x- )•(
)•( x-1)=
x-1)= (x-2)2,
(x-2)2,∴
 =
= =
= ,
,4x2-25x+25=0,
解得:x1=
 (因为分成边长为1的正三角形,所以此数不符合舍去),x2=5,
(因为分成边长为1的正三角形,所以此数不符合舍去),x2=5,∴△ABC的周长是3×5=15,
故答案为:15.
点评:本题考查了菱形的性质,等边三角形的性质,熟练掌握有一个角等于60°的菱形的两条对角线的关系是解题的关键,本题难点在于根据三角形的面积与菱形的面积列出方程.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
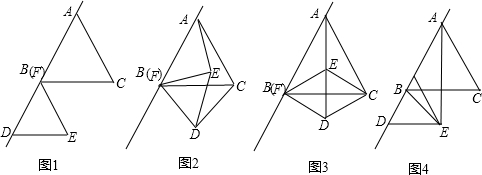
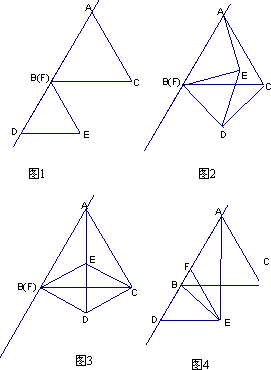
 ,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
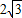 ,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
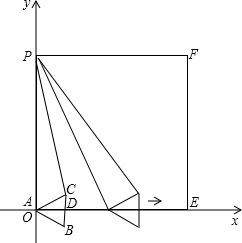
,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由; cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.