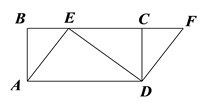äãá¢áÖàï
Àƒäãá¢À¢àÓë¥1ȘØîøˆéæöÿüÔ![]() ÆŠéæöÿüÔ
ÆŠéæöÿüÔ![]() çáÅöæÇüÁë˜È˜¢ˆ¢Öñ§ü·üÁñÇȘúØüÁ§£ÆÖçÐ
çáÅöæÇüÁë˜È˜¢ˆ¢Öñ§ü·üÁñÇȘúØüÁ§£ÆÖçÐ![]() ¤ëçÐ
¤ëçÐ![]() ÈÛéæöÿüÔ
ÈÛéæöÿüÔ![]() ÆŠ
ÆŠ![]() øÃí»¯Šøç£ÆÖçÐ
øÃí»¯Šøç£ÆÖçÐ![]() öˆéæöÿüÔ
öˆéæöÿüÔ![]() èü
èü![]() ê§çÐ¥ðØ£Ñ₤çÐȘ¿»çÐ
ê§çÐ¥ðØ£Ñ₤çÐȘ¿»çÐ![]() æ¼øÝüÔ
æ¼øÝüÔ![]() øÃȘƊ
øÃȘƊ![]() §£ÆÖçÐ
§£ÆÖçÐ![]() ÈÛ
ÈÛ
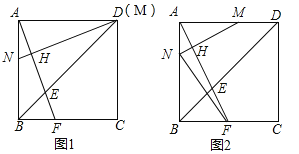
È´1ÈˋúµéæöÿüÔ![]() ÆŠéæöÿüÔ
ÆŠéæöÿüÔ![]() çá§ãö—ò§;
çá§ãö—ò§;
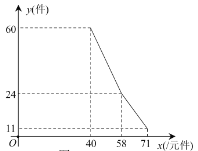
È´2ÈˋùáÝÔÅö![]() çáûÌ£»öˆ
çáûÌ£»öˆ![]() Șúµ
Șúµ![]() çáæŸÇµøçȘýÂÅÇ°—ÇùòÝçÐ
çáæŸÇµøçȘýÂÅÇ°—ÇùòÝçÐ![]() çáæ½Ýõ;
çáæ½Ýõ;
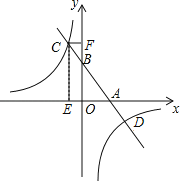
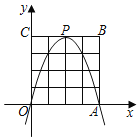
È´3ÈˋàÓë¥2Ș![]() çáÑå°óøÃöˆøÝüÔ
çáÑå°óøÃöˆøÝüÔ![]() Ș
Ș![]() Ɗ
ÆŠ![]() §£ÆÖçÐ
§£ÆÖçÐ![]() ȘåÖ(2)çáä¾¥±üôȘøÝüÔ
ȘåÖ(2)çáä¾¥±üôȘøÝüÔ![]() èüòúñþÇÌåÖØ£çÐ
èüòúñþÇÌåÖØ£çÐ![]() Șò¿çûØå
Șò¿çûØå![]() öˆÑËçÐçá໧úÅöÆŠ
öˆÑËçÐçá໧úÅöÆŠ![]() üÁùóÈ¢àÓ¿«ÇÌåÖȘúµ°—çÐ
üÁùóÈ¢àÓ¿«ÇÌåÖȘúµ°—çÐ![]() çáæ½ÝõÈ£àÓ¿«ý£ÇÌåÖȘùçû¼âÚÆè.
çáæ½ÝõÈ£àÓ¿«ý£ÇÌåÖȘùçû¼âÚÆè.
ÀƒÇÞ¯¡À¢È´1Èˋ![]() È£
È£![]() ȣȴ2Èˋ16ȣȴ-1,4ÈˋÈ£ È´3ÈˋÇÌåÖçÐ
ȣȴ2Èˋ16ȣȴ-1,4ÈˋÈ£ È´3ÈˋÇÌåÖçÐ![]() çáæ½Ýõ
çáæ½Ýõ![]() £·È´
£·È´![]() ò¿çû
ò¿çû![]() öˆÑËçÐçá໧úÅöÆŠ
öˆÑËçÐçá໧úÅöÆŠ![]() üÁùóȘâÚÆ襫§ãö—ÈÛ
üÁùóȘâÚÆ襫§ãö—ÈÛ
Àƒ§ãö—À¢
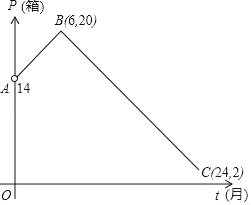
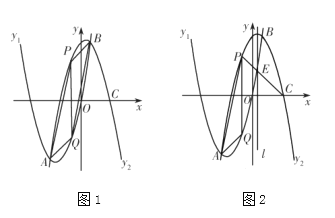
È´1ÈˋñøÝÞâ«ÆûǻѴüçò»ñ´úµê§¡—ѱÇö¤₤ò»çá§ãö—ò§È£
È´2ÈˋèÒçÐP¤Ãæ½ÝõöˆtȘå·PÈ´tȘt2ȨtȨ6ÈˋȘQÈ´tȘt2Ȩ5tÈˋȘÝÚòƒPQçá°ÊȘ¡ªƒïê§à»§úÅöûÌ£»¤ë¢èçûSÆŠtçá¿Äüçò§È˜éðñ§¤µ¢èçûSçáæŸÇµøçÈ£
È´3ÈˋüààñÑ´ÀüAQBȧ135ÀÐȘࣤµñøê§øøúÕ¢—äøôÜ¢èçû§ÃôÜÈÛ
§ãȤȴ1Èˋ§¨![]() ǺàŠ
ǺàŠ![]() çûȤ
çûȤ![]() Ș
Ș
ÀÁ![]() Ș
Ș
ÀÔ![]() ÆŠ
ÆŠ![]() ÅöæÇüÁë˜È˜¢ˆ¢ÖüÁñÇȘ
ÅöæÇüÁë˜È˜¢ˆ¢ÖüÁñÇȘ
ÀÁ![]() Ș
Ș
ÀÁ![]() Ș
Ș
§¨![]() ǺàŠçûȘ
ǺàŠçûȘ
![]()
§ãçûȤ![]() Ș
Ș![]() Ș
Ș
ÀÁ![]() È£
È£
È´2ÈˋèÒçÐ![]() ¤Ãæ½ÝõöˆtȘ
¤Ãæ½ÝõöˆtȘ
å·![]() Ș
Ș![]() Ș
Ș
ÀÁ![]() Ș
Ș
ÀÁ![]()
![]() Ș
Ș
ÀÁçÝ![]() òÝȘ
òÝȘ![]() ȘÇùòÝ
ȘÇùòÝ![]() çáæ½Ýõöˆ
çáæ½Ýõöˆ![]() È£
È£
È´3ÈˋÇÌåÖçÐ![]() Ș
Ș
Æè![]() çûøÝüÔ
çûøÝüÔ![]() öˆÈ¤
öˆÈ¤![]() Ș
Ș
ÆèÈ´2Èˋøˆ![]() çÐçáæ½Ýõöˆ
çÐçáæ½Ýõöˆ![]() çÐçáæ½Ýõöˆ
çÐçáæ½Ýõöˆ![]() Ș
Ș
úØ![]() öˆ
öˆ![]() ,
,
êŸ![]() çûȤ
çûȤ![]() öˆ
öˆ![]() Ș
Ș
àÓë¥È˜èÒ![]() ÆŠ
ÆŠ![]() øç£ÆÖçÐ
øç£ÆÖçÐ![]() ȘøÝüÔ
ȘøÝüÔ![]() ÆŠ
ÆŠ![]() øç£ÆÖçÐ
øç£ÆÖçÐ![]() Ș
Ș
æ¼![]() çáîÆ°ÊüÔȘǿæÐöˆçÐ
çáîÆ°ÊüÔȘǿæÐöˆçÐ![]() ȘØæøˆ
ȘØæøˆ![]() Ș
Ș
ÀÁ![]() Ș
Ș
ÀÁ![]() Ș
Ș
ÀÔ![]() Ș
Ș
ÀÁ![]() Ș
Ș
ÀÁ![]() çÐåÖ
çÐåÖ![]() çáèüñ§
çáèüñ§![]() Ș
Ș
![]() Ș
Ș ![]() Ș
Ș
![]() ,
,![]() Ș
Ș
Âìà¶![]() Șå·
Șå·![]() Ș
Ș
¥Ç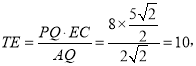
ÇùòÝ![]() çáæ½Ýõöˆ
çáæ½Ýõöˆ![]() È£
È£
ÂÖà¶![]() Șå·
Șå·![]() Ș
Ș
¥Ç![]() ȘÇùòÝ
ȘÇùòÝ![]() çáæ½Ýõöˆ
çáæ½Ýõöˆ![]() Ș
Ș
æÜèü¢èøˆÇÌåÖçÐ![]() çáæ½Ýõ
çáæ½Ýõ![]() £·È´
£·È´![]() ò¿çû
ò¿çû![]() öˆÑËçÐçá໧úÅöÆŠ
öˆÑËçÐçá໧úÅöÆŠ![]() üÁùóÈÛ
üÁùóÈÛ
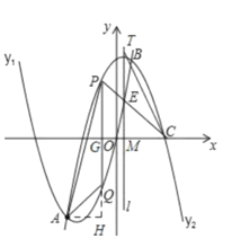

 û«ÅÈ¢öäûüçêÅÇÞ¯¡
û«ÅÈ¢öäûüçêÅÇÞ¯¡