题目内容
 等腰三角形ABC中,AB=BC=10,∠A=50°,∠ABC的平分线交AC边于点D,过D作DE∥BC交AB于点E.
等腰三角形ABC中,AB=BC=10,∠A=50°,∠ABC的平分线交AC边于点D,过D作DE∥BC交AB于点E.
(1)求∠DBC的度数;(2)求DE的长.
解:(1)∵AB=BC,
∴∠A=∠C=50°,
∴∠ABC=80°,
∴BD平分∠ABC,
∴∠DBC=40°;
(2)∵DE∥BC,
∴∠EDB=∠DBC=40°,
∴ED=EB,
∴∠A=∠ADE=50°,
∴AE=ED,
∴AE=EB,DE=5.
分析:(1)根据等腰三角形的性质得出BD平分∠ABC,即可的得出答案;
(2)根据等腰三角形的性质以及平行线的性质得出ED=EB,进而得出AE=EB即可得出答案.
点评:此题主要考查了平行线的性质以及等腰三角形的性质,根据题意灵活应用等腰三角形的三线合一是解决问题的关键.
∴∠A=∠C=50°,
∴∠ABC=80°,
∴BD平分∠ABC,
∴∠DBC=40°;
(2)∵DE∥BC,
∴∠EDB=∠DBC=40°,
∴ED=EB,
∴∠A=∠ADE=50°,
∴AE=ED,
∴AE=EB,DE=5.
分析:(1)根据等腰三角形的性质得出BD平分∠ABC,即可的得出答案;
(2)根据等腰三角形的性质以及平行线的性质得出ED=EB,进而得出AE=EB即可得出答案.
点评:此题主要考查了平行线的性质以及等腰三角形的性质,根据题意灵活应用等腰三角形的三线合一是解决问题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
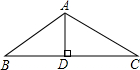 如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD=
如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD= 如图,等腰三角形ABC中,AB=AC,AD是底边BC上的中线,若AB=10,BC=12,则中线AD的长度为( )
如图,等腰三角形ABC中,AB=AC,AD是底边BC上的中线,若AB=10,BC=12,则中线AD的长度为( )