题目内容
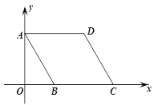
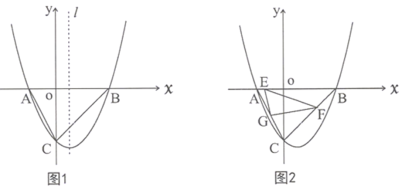
【题目】如图1,已知抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且![]() .
.
(1)求该抛物线的函数表达式;
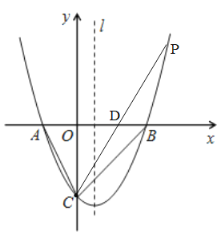
(2)设P是(1)中抛物线上的一个动点,当直线OC平分∠ACP时,求点P的坐标;
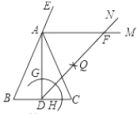
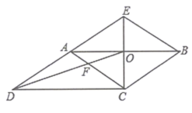
(3)如图2,点G是线段AC的中点,动点E从点A出发,以每秒1个单位长度的速度向终点B运动,动点F从点B出发,以每秒![]() 个单位长度的速度向终点C运动,若E、F两点同时出发,运动时间为t秒.则当t为何值时,
个单位长度的速度向终点C运动,若E、F两点同时出发,运动时间为t秒.则当t为何值时,![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]()
【解析】
(1)根据OA、OB的长度求出点A、B的坐标,然后利用待定系数法求二次函数解析式解答;
(2)设![]() 与
与![]() 轴相交于点
轴相交于点![]() ,先求出C,D的坐标,再求出直线
,先求出C,D的坐标,再求出直线![]() 的解析式,联立抛物线的函数表达式得出方程组,解方程组即可得点P的坐标;
的解析式,联立抛物线的函数表达式得出方程组,解方程组即可得点P的坐标;
(3)先求出t的取值范围,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,用t表示出BM的长度,然后用t表示出EH、HM、EM的长度,分两种情况求出
,用t表示出BM的长度,然后用t表示出EH、HM、EM的长度,分两种情况求出![]() 的面积,求出△ABC的面积,根据
的面积,求出△ABC的面积,根据![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 列出关于t的方程,解方程即可求解.
列出关于t的方程,解方程即可求解.
解:(1)∵![]()
∴![]()
把![]() 分别代入
分别代入![]() 得:
得:
![]()
解得:![]()
∴![]()
(2)如图,设![]() 与
与![]() 轴相交于点
轴相交于点![]()
∵![]() 平分
平分![]() ,
,![]() ⊥
⊥![]()
∴![]()
∴![]()
把![]() 代入
代入![]() 得
得![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]()
把![]() 分别代入
分别代入![]() 得
得
![]()
解得:![]()
∴![]()
依题意得
解得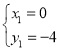 ,
,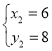
∴![]()
(3)如图,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]()
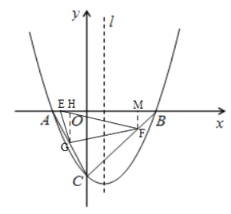
∵![]() ∥
∥![]() 轴
轴
∴![]() ∽
∽![]()
∴![]()
∴由![]()
得![]()
点![]() 运动到点
运动到点![]() 的时间为
的时间为![]() 秒,
秒,
点![]() 运动到点
运动到点![]() 的时间为
的时间为![]() 秒
秒
当![]() 时,如图
时,如图
过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]()
依题意得:![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
![]()
![]() 或
或![]()
∵![]()
![]() 的面积是
的面积是![]() 的面积的
的面积的![]()
∴![]() 或
或![]() =
=![]()
解得:![]() (舍去)或
(舍去)或![]() (舍去)
(舍去)
当![]() 时,如图
时,如图
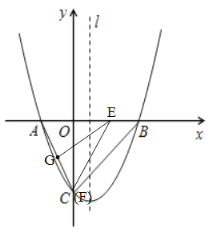
![]()
![]()
![]()
∴![]()
综上所述,当![]() 或
或![]() 时,
时,![]() 的面积是
的面积是![]() 的面积的
的面积的![]() .
.

【题目】经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |
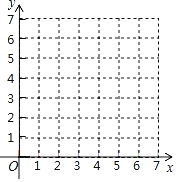
(1)请画出相应函数的图象,并求出函数表达式.
(2)点A(x1,y1),B(x2,y2)在此函数图象上.若x1<x2,则y1,y2有怎样的大小关系?请说明理由.