题目内容
如图,已知△ABC的三个顶点坐标分别为A(-4,0),B(1,0),C(-2,6).
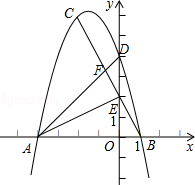
(1)求经过点A,B,C三点的抛物线解析式.
(2)设直线BC交y轴于点E,连结AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连结AD交BC于点F,求证:以A,B,F为顶点的三角形与△ABC相似,并求: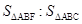 .
.

(1)求经过点A,B,C三点的抛物线解析式.
(2)设直线BC交y轴于点E,连结AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连结AD交BC于点F,求证:以A,B,F为顶点的三角形与△ABC相似,并求:
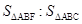 .
.(1) ;(2)证明见试题解析;(3)证明见试题解析,
;(2)证明见试题解析;(3)证明见试题解析, .
.
 ;(2)证明见试题解析;(3)证明见试题解析,
;(2)证明见试题解析;(3)证明见试题解析, .
.试题分析:(1)利用待定系数发求解即可得出抛物线的解析式;
(2)求出直线BC的函数解析式,从而得出点E的坐标,然后分别求出AE及CE的长度即可证明出结论;
(3)求出AD的函数解析式,然后结合直线BC的解析式可得出点F的坐标,由题意得∠ABF=∠CBA,然后判断出
 是否等于
是否等于 即可作出判断.
即可作出判断.试题解析:(1)设函数解析式为:
 ,由函数经过点A(﹣4,0)、B(1,0)、C(﹣2,6),
,由函数经过点A(﹣4,0)、B(1,0)、C(﹣2,6),可得
 ,解得:
,解得: ,故经过A、B、C三点的抛物线解析式为:
,故经过A、B、C三点的抛物线解析式为: ;
;(2)设直线BC的函数解析式为y=kx+b,由题意得:
 ,解得:
,解得: ,即直线BC的解析式为
,即直线BC的解析式为 .故可得点E的坐标为(0,2),从而可得:AE=
.故可得点E的坐标为(0,2),从而可得:AE= ,CE=
,CE= ,故可得出AE=CE;
,故可得出AE=CE;(3)相似.理由如下:设直线AD的解析式为y=kx+b,则
 ,解得:
,解得: ,即直线AD的解析式为
,即直线AD的解析式为 .联立直线AD与直线BC的函数解析式可得:
.联立直线AD与直线BC的函数解析式可得: ,解得:
,解得: ,即点F的坐标为(
,即点F的坐标为( ,
, ),则BF=
),则BF= ,又∵AB=5,BC=
,又∵AB=5,BC= ,∴
,∴ ,
, ,∴
,∴ ,又∵∠ABF=∠CBA,∴△ABF∽△CBA.故以A、B、F为顶点的三角形与△ABC相似,
,又∵∠ABF=∠CBA,∴△ABF∽△CBA.故以A、B、F为顶点的三角形与△ABC相似,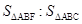 =
= .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目




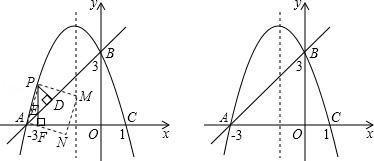
 与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为 .
与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为 .
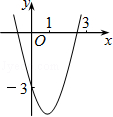
 (a≠0)的图像如图所示,若
(a≠0)的图像如图所示,若 (k≠0)有两个不相等的实数根,则k的取值范围是( )
(k≠0)有两个不相等的实数根,则k的取值范围是( ) 




 (
( >0)的对称轴为直线
>0)的对称轴为直线 ,且经过点(-3,
,且经过点(-3,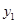 ),(4,
),(4,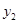 ),试比较
),试比较