题目内容
(2000•山东)如图,⊙O′的弦AB是⊙O的直径,点O′在⊙O上,设图中两个阴影部分的面积分别为S和S′,则S′:S= .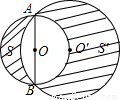
【答案】分析:设小圆的半径为R,则大圆的半径为 R,分别求得两个阴影部分的面积后计算.
R,分别求得两个阴影部分的面积后计算.
解答: 解:如图,设小圆半径OO′=R,则△ABO′是等腰直角三角形,大圆半径AO′=
解:如图,设小圆半径OO′=R,则△ABO′是等腰直角三角形,大圆半径AO′= R,
R,
S△ABO′= AB•OO′=R2,S扇形O′AB=
AB•OO′=R2,S扇形O′AB= •π•(
•π•( R)2=
R)2= πR2,
πR2,
S小半圆的面积O′AB= πR2,
πR2,
∴空白部分的面积=2× πR2-R2=πR2-R2,
πR2-R2=πR2-R2,
∴S=πR2-(πR2-R2)=R2,
S′=π•( R)2-(πR2-R2)=πR2+R2,
R)2-(πR2-R2)=πR2+R2,
∴S′:S=(πR2+R2):R2=π+1.
故本题答案为:π+1.
点评:本题考查了圆的面积公式,扇形的面积公式,等腰直角三角形的面积公式.关键是表示出空白部分的面积.
 R,分别求得两个阴影部分的面积后计算.
R,分别求得两个阴影部分的面积后计算.解答:
 解:如图,设小圆半径OO′=R,则△ABO′是等腰直角三角形,大圆半径AO′=
解:如图,设小圆半径OO′=R,则△ABO′是等腰直角三角形,大圆半径AO′= R,
R,S△ABO′=
 AB•OO′=R2,S扇形O′AB=
AB•OO′=R2,S扇形O′AB= •π•(
•π•( R)2=
R)2= πR2,
πR2,S小半圆的面积O′AB=
 πR2,
πR2,∴空白部分的面积=2×
 πR2-R2=πR2-R2,
πR2-R2=πR2-R2,∴S=πR2-(πR2-R2)=R2,
S′=π•(
 R)2-(πR2-R2)=πR2+R2,
R)2-(πR2-R2)=πR2+R2,∴S′:S=(πR2+R2):R2=π+1.
故本题答案为:π+1.
点评:本题考查了圆的面积公式,扇形的面积公式,等腰直角三角形的面积公式.关键是表示出空白部分的面积.

练习册系列答案
相关题目









 p
p p
p



