题目内容
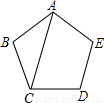
（2000•山东）如图，等腰梯形ABCD中，AB∥CD，对角线AC垂直于一腰BC，且AC平分∠BAD，若梯形的中位线长为p，则梯形ABCD的周长为（ ）
A．
pB．3p
C．
pD．4p
【答案】分析：根据平行线的性质及等角对等边可得到AD=CD=BC，根据角平分线的性质可得到AB=2BC，从而根据中位线的性质及已知即可求得梯形的周长．
解答：解：∵AB∥CD
∴∠DCA=∠BAC
∵AC平分∠BAD
∴∠DAC=∠CAB
∴∠DAC=∠DCA
∴AD=DC=BC
∵∠CAB=
∠DAB=
∠B，∠ACB=90°
∴∠CAB=30°
∴AB=2BC
∵
（AB+DC）=p
（2DC+DC）=p
∴DC=
p
∵梯形ABCD的周长=AB+BC+CD+AD=5CD=
p．
故选C．
点评：此题主要考查学生对中位线的性质及直角三角形的性质的综合运用．
解答：解：∵AB∥CD
∴∠DCA=∠BAC
∵AC平分∠BAD
∴∠DAC=∠CAB
∴∠DAC=∠DCA
∴AD=DC=BC
∵∠CAB=
∠DAB=∠B，∠ACB=90°∴∠CAB=30°
∴AB=2BC
∵
（AB+DC）=p（2DC+DC）=p∴DC=
p∵梯形ABCD的周长=AB+BC+CD+AD=5CD=
p．故选C．
点评：此题主要考查学生对中位线的性质及直角三角形的性质的综合运用．
练习册系列答案
相关题目
