题目内容
已知m是方程x2-x-1=0的一个根，则代数式2m2-2m的值是 ．
考点：一元二次方程的解
专题：
分析：由m是方程x2-x-1=0的一个根，将x=m代入方程得到关于m的等式，变形后即可求出所求式子的值．
解答：解：∵m是方程x2-x-1=0的一个根，
∴将x=m代入方程得：m2-m-1=0，
则m2-m=1．
∴2m2-2m=2（m2-m）=2×1=2．
故答案为：2．
∴将x=m代入方程得：m2-m-1=0，
则m2-m=1．
∴2m2-2m=2（m2-m）=2×1=2．
故答案为：2．
点评：此题考查了一元二次方程的解的定义．此题应注意把（m2-m）当成一个整体．利用了整体的思想．
练习册系列答案
相关题目
已知点A（xl，y1）、B（x1-1，y2）在直线y=-2x+3上，则y1与y2的大小关系是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、yl=y2 |
| D、y1与y2的大小关系不定 |
二次函数y=ax2+bx+c的图象如图所示，现有以下结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b≥m（am+b）．
其中正确的结论有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
如图：等边△ABC中，D在射线BA上，以CD为一边，向右上作等边△EDC，连结AE．若BC、CD的长为方程x2-15x+7m=0的两根，当m为符合题意的最大的整数时，则不同位置的D点共有
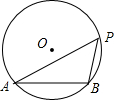如图，A、B两点在⊙O上，点P为⊙O上的动点，当弦AB的长度小于⊙O半径的长度，要使△ABP为等腰三角形，则所有符合条件的点P有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
如图，平面直角坐标系中，已知B（-3，0），C（3，0），点A（0，m）在y