Question

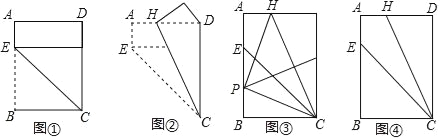
【题目】如图，正方形ABCD的边长为2,.过B作BE//AC.

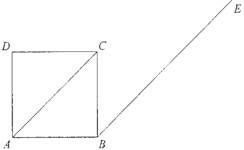
(1)求BE与AC之间的距离；

(2)F为BE上一点，连接AF，过C作CG//AF交BE于G.若∠FAB=15°,

①依题意补全图形;

②求证:四边形AFGC是菱形.

Answer 1

【答案】（1）；（2）①见解析；②见解析.

【解析】

（1）连结BD交AC于O点，如图，利用正方形的性质得到AC⊥BD，BO＝，由于BE∥AC，于是可判断BE与AC之间的距离为；

（2）①根据几何语言画出对应图形；

②设OB与AF交于点H，先证明四边形AFGC是平行四边形，再计算出AH＝，HF＝，从而得到AF＝AH＋HF＝2＝AC，于是可判断四边形AFGC是菱形．

解：（1）连结BD交AC于O点，如图，

∵四边形ABCD为正方形，

∴AC⊥BD，BO＝BD＝×2＝，

∵BE∥AC，

∴OB⊥BE，

∴BE与AC之间的距离为，

故答案为：；

（2）①如图，四边形AFGC为所作；

②设OB与AF交于点H，

∵CG∥AF，AC∥FG，

∴四边形AFGC是平行四边形，

∵四边形ABCD为正方形，

∴OA＝OB＝，AC＝2，∠AOB＝90°，∠OAB＝45°，

∵∠FAB＝15°，

∴∠OAF＝30°，

在Rt△OAH中，OH＝OA＝，AH＝2OH＝，

∴BH＝OH＝，

∵AC∥BE，

∴∠BFA＝∠OAF＝30°，

∴HF＝2BH＝2（）＝2，

∴AF＝AH＋HF＝＋2＝2，

∴AC＝AF，

∴四边形AFGC是菱形．