题目内容
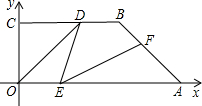
如图,OA是⊙O的半径,AB是弦,OA:AB=5:8,则sin∠OAB= .
【答案】分析:根据比例,先表示出弦心距,再利用勾股定理即可求解.
解答: 解:过O作OC⊥AB于C.
解:过O作OC⊥AB于C.
由垂径定理得AC=BC.
∵OA:AB=5:8,
∴设OA=5x,则AB=8x,AC=4x,
OC= =
= =3x,
=3x,
sin∠OAB= =
= =
= .
.
点评:此题比较简单,考查垂径定理及锐角三角函数的定义.
解答:
 解:过O作OC⊥AB于C.
解:过O作OC⊥AB于C.由垂径定理得AC=BC.
∵OA:AB=5:8,
∴设OA=5x,则AB=8x,AC=4x,
OC=
 =
= =3x,
=3x,sin∠OAB=
 =
= =
= .
.点评:此题比较简单,考查垂径定理及锐角三角函数的定义.

练习册系列答案
相关题目

 上的点E处.
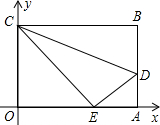
上的点E处. 如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD= 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.