题目内容
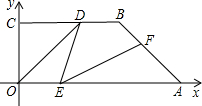
 如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=| 1 |
| 4 |
| 2 |
| 17 |
| 8 |
41
| ||
| 4 |
| 17 |
| 8 |
41
| ||
| 4 |
分析:若△AEF是等腰三角形,应分三种情况讨论:
①AF=EF,此时△AEF是等腰Rt△,A′在AB的延长线上,重合部分是四边形EDBF,其面积可由梯形ABDE与△AEF的面积差求得;
②AE=EF,此时△AEF是等腰Rt△,且E是直角顶点,此时重合部分即为△A′EF,由于∠DEF=∠EFA=45°,得DE∥AB,即四边形AEDB是平行四边形,则AE=BD,进而可求得重合部分的面积;
③AF=AE,此时四边形AEA′F是菱形,重合部分是△A′EF;由△ODE∽△AEF,那么此时OD=OE=3,由此可求得AE、AF的长,过F作x轴的垂线,即可求出△AEF中AE边上的高,进而可求得△AEF(即△A′EF)的面积.
①AF=EF,此时△AEF是等腰Rt△,A′在AB的延长线上,重合部分是四边形EDBF,其面积可由梯形ABDE与△AEF的面积差求得;
②AE=EF,此时△AEF是等腰Rt△,且E是直角顶点,此时重合部分即为△A′EF,由于∠DEF=∠EFA=45°,得DE∥AB,即四边形AEDB是平行四边形,则AE=BD,进而可求得重合部分的面积;
③AF=AE,此时四边形AEA′F是菱形,重合部分是△A′EF;由△ODE∽△AEF,那么此时OD=OE=3,由此可求得AE、AF的长,过F作x轴的垂线,即可求出△AEF中AE边上的高,进而可求得△AEF(即△A′EF)的面积.
解答:解:当△AEF为等腰三角形时,存在EF=AF或EF=AE或AF=AE共3种情况;
①当EF=AF时,如图(1),

∠FAE=∠FEA=∠DEF=45°;
∴△AEF为等腰直角三角形,D在A′E上(A′E⊥OA),
B在A′F上(A′F⊥EF),
∴△A′EF与五边形OEFBC重叠的面积为四边形EFBD的面积;
∵AE=OA-OE=OA-CD=4
-
=
,
∴AF=AE•sin45°=
×
=
,
S△AEF=
EF×AF=
×(
)2=
,
∴S梯形AEDB=
(BD+AE)•DE=
×(
+
)×
=
,
∴S四边形BDEF=S梯形AEDB-S△AEF=
-
=
;
(也可用S阴影=S△A'EF-S△A'BD),
②当EF=AE时,如图(2),

此时△A′EF与五边形OEFBC重叠部分面积为△A′EF面积.
∠DEF=∠EFA=45°,DE∥AB,又DB∥EA,
∴四边形DEAB是平行四边形
∴AE=DB=
,
∴S△A′EF=S△AEF=
×(
)2=1;
③当AF=AE时,如图(3),

四边形AEA′F为菱形且△A′EF在五边形OEFBC内.
∴此时△A′EF与五边形OEFBC重叠部分面积为△A′EF面积.
易得△ODE∽△AEF,则OD=OE=3,
∴AE=AF=OA-OE=4
-3,
过F作FH⊥AE于H,则FH=AF•sin45°=(4
-3)×
=4-
,
∴S△A′EF=S△AEF=
AE•FH=
×(4
-3)•(4-
)=
,
综上所述,△A′EF与五边形OEFBC重叠部分的面积为
或1或
.
故答案为:
或1或
.
①当EF=AF时,如图(1),

∠FAE=∠FEA=∠DEF=45°;
∴△AEF为等腰直角三角形,D在A′E上(A′E⊥OA),
B在A′F上(A′F⊥EF),
∴△A′EF与五边形OEFBC重叠的面积为四边形EFBD的面积;
∵AE=OA-OE=OA-CD=4
| 2 |
| 3 |
| 2 |
| 2 |
| 5 |
| 2 |
| 2 |
∴AF=AE•sin45°=
5
| ||
| 2 |
| ||
| 2 |
| 5 |
| 2 |
S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
∴S梯形AEDB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
5
| ||
| 2 |
3
| ||
| 2 |
| 21 |
| 4 |
∴S四边形BDEF=S梯形AEDB-S△AEF=
| 21 |
| 4 |
| 25 |
| 8 |
| 17 |
| 8 |
(也可用S阴影=S△A'EF-S△A'BD),
②当EF=AE时,如图(2),

此时△A′EF与五边形OEFBC重叠部分面积为△A′EF面积.
∠DEF=∠EFA=45°,DE∥AB,又DB∥EA,
∴四边形DEAB是平行四边形
∴AE=DB=
| 2 |
∴S△A′EF=S△AEF=
| 1 |
| 2 |
| 2 |
③当AF=AE时,如图(3),

四边形AEA′F为菱形且△A′EF在五边形OEFBC内.
∴此时△A′EF与五边形OEFBC重叠部分面积为△A′EF面积.
易得△ODE∽△AEF,则OD=OE=3,
∴AE=AF=OA-OE=4
| 2 |
过F作FH⊥AE于H,则FH=AF•sin45°=(4
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴S△A′EF=S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
41
| ||
| 4 |
综上所述,△A′EF与五边形OEFBC重叠部分的面积为
| 17 |
| 8 |
41
| ||
| 4 |
故答案为:
| 17 |
| 8 |
41
| ||
| 4 |
点评:此题考查了四边形综合题,涉及了梯形、平行四边形、等腰三角形的性质,以及相似三角形的判定和性质,难度较大,注意分类讨论思想的运用.

练习册系列答案
相关题目

 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y= 如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=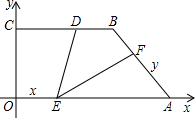 是BC上一点,BD=
是BC上一点,BD=