题目内容
【题目】如图,长方形OABC的边OC、OA分别在x轴、y轴上,点B的坐标为(![]() ,1)点D是AB边上一个动点(与点A不重合),沿OD将△OAD对折后,点A落到点P处,并满足△PCB是等腰三角形,则P点坐标为________.
,1)点D是AB边上一个动点(与点A不重合),沿OD将△OAD对折后,点A落到点P处,并满足△PCB是等腰三角形,则P点坐标为________.

【答案】(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】
连接PB,PC.分三种情况:①若PB=PC,设P(x,![]() ),过P作PH⊥x轴于H.在Rt△OPH中根据勾股定理解得x,从而确定P点坐标;②若BP=BC,则BP=1,连接OB.在Rt△OBC中根据勾股定理求出OB,从而得出P为线段OB中点,求出P点坐标;③若CP=CB,则CP=1,PO=PC,P在OC中垂线上.设P(
),过P作PH⊥x轴于H.在Rt△OPH中根据勾股定理解得x,从而确定P点坐标;②若BP=BC,则BP=1,连接OB.在Rt△OBC中根据勾股定理求出OB,从而得出P为线段OB中点,求出P点坐标;③若CP=CB,则CP=1,PO=PC,P在OC中垂线上.设P(![]() ,y),过P作PH⊥x轴于H,在Rt△OPH中根据勾股定理求出P点坐标即可.
,y),过P作PH⊥x轴于H,在Rt△OPH中根据勾股定理求出P点坐标即可.
解:连接PB,PC,
①若PB=PC,则P在BC的中垂线y=![]() 上,
上,
∴设P(x,![]() ),
),
如图,过P作PH⊥x轴于H,
在Rt△OPH中,PH=![]() ,OH=x,OP=1,
,OH=x,OP=1,
∴x2+![]() =1,
=1,
解得:x1=![]() ,x2=-
,x2=-![]() (不合题意),
(不合题意),
∴P(![]() ,
,![]() );
);
②若BP=BC,则BP=1,连接OB,
∵OP=1,
∴OP+PB=2,
∵在Rt△OBC中,∠OCB=90°,OB=![]() =2,
=2,
∴OP+PB=OB,
∴O,P,B三点共线,P为线段OB中点.
又∵B(![]() ,1),
,1),
∴P(![]() ,
,![]() );
);
③若CP=CB,则CP=1,
∵OP=1,
∴PO=PC,则P在OC的中垂线x=![]() 上,
上,
∴设P(![]() ,y).
,y).
过P作PH⊥x轴于H,在Rt△OPH中,PH=|y|,OH=![]() ,OP=1,
,OP=1,
∴y2+![]() =1,
=1,
解得:y1=![]() ,y2=-
,y2=-![]() ,
,
∴P(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ),
),
当点P(![]() ,-
,-![]() )时,∠AOP=120°,此时∠AOD=60°,点D与点B重合,符合题意.
)时,∠AOP=120°,此时∠AOD=60°,点D与点B重合,符合题意.
故答案为:(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).

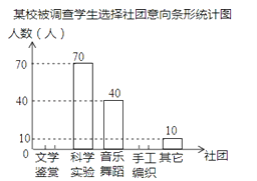
【题目】为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的人数.