题目内容
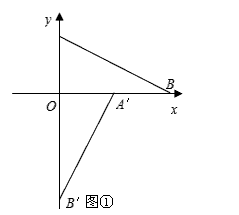
如图①,点A′,B′的坐标分别为(2,0)和(0,-4),将△A′B′O绕点O按逆时针方向旋90°转后得△ABO,点A′的对应点是点A,点B′的对应点是点B。
(1)写出A,B两点的坐标,并求出直线AB的解析式;
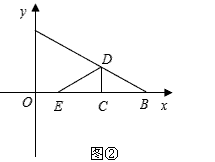
(2)将△ABO沿着垂直于x轴的线段CD折叠,(点C在x轴上,点D在AB上,点D不与A,B重合)如图②,使点B落在x轴上,点B的对应点为点E,设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S。
i)试求出S与x之间的函数关系式(包括自变量x的取值范围);
ii)当x为何值时,S的面积最大?最大值是多少?
iii)是否存在这样的点C,使得△ADE为直角三角形?若存在,直接写出点C的坐标;若不存在,请说明理由。
(1)写出A,B两点的坐标,并求出直线AB的解析式;
(2)将△ABO沿着垂直于x轴的线段CD折叠,(点C在x轴上,点D在AB上,点D不与A,B重合)如图②,使点B落在x轴上,点B的对应点为点E,设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S。
i)试求出S与x之间的函数关系式(包括自变量x的取值范围);
ii)当x为何值时,S的面积最大?最大值是多少?
iii)是否存在这样的点C,使得△ADE为直角三角形?若存在,直接写出点C的坐标;若不存在,请说明理由。
解:(1)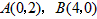 ,
,
设直线AB的解析式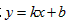 ,
,
则有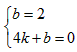 ,解得
,解得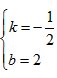
∴直线AB的解析式为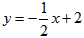 ;
;
(2)i)①点E在原点和x轴正半轴上时,重叠部分是 ,
,
则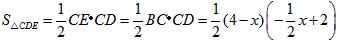
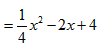
当E与O重合时,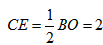 ,
,
∴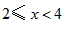
②当E在x轴的负半轴上时,设DE与y轴交于点F,则重叠部分为梯形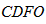 ,
,
∴
∴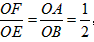
∴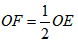
又∵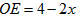 ,
,
∴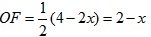
∴
当点C与点O重合时,点C的坐标为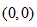 ,
,
∴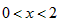
综合①②得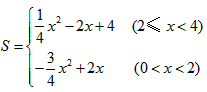 ;
;
ii)①当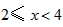 时,
时,
∴ 对称轴是x=4,
∵抛物线开口向上,
∴在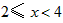 中,S随x的增大而减小,
中,S随x的增大而减小,
∴当x=2时,S的最大值= ,
,
②当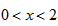 时,
时,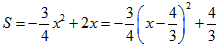
∴对称轴是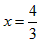
∵抛物线开口向下,
∴当 时,S有最大值为
时,S有最大值为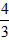 ,
,
∴综合①②当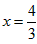 时,S有最大值为
时,S有最大值为
iii)存在,点C的坐标为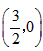 和
和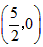
详解:①当 以点A为直角顶点时,作
以点A为直角顶点时,作 交x轴负半轴于点E,
交x轴负半轴于点E,
∵
∴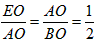
∵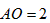
∴
∴点E坐标为(-1,0),
∴点C的坐标为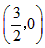
②当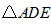 以点E为直角顶点时,同样有
以点E为直角顶点时,同样有
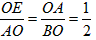
∴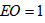
∴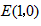
∴点C的坐标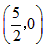 ,
,
综合①②知满足条件的坐标有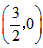 和
和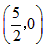 。
。
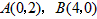 ,
,设直线AB的解析式
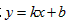 ,
,则有
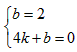 ,解得
,解得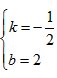
∴直线AB的解析式为
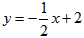 ;
;(2)i)①点E在原点和x轴正半轴上时,重叠部分是
 ,
,则
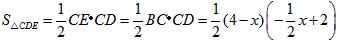
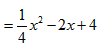
当E与O重合时,
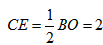 ,
,∴
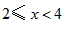
②当E在x轴的负半轴上时,设DE与y轴交于点F,则重叠部分为梯形
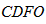 ,
,∴

∴
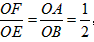
∴
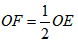
又∵
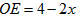 ,
,∴
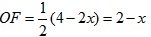
∴

当点C与点O重合时,点C的坐标为
 ,
,∴
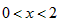
综合①②得
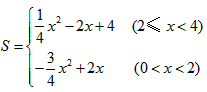 ;
;ii)①当
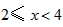 时,
时,
∴ 对称轴是x=4,
∵抛物线开口向上,
∴在
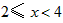 中,S随x的增大而减小,
中,S随x的增大而减小,∴当x=2时,S的最大值=
 ,
,②当
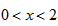 时,
时,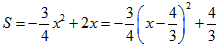
∴对称轴是
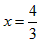
∵抛物线开口向下,
∴当
 时,S有最大值为
时,S有最大值为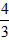 ,
,∴综合①②当
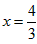 时,S有最大值为
时,S有最大值为
iii)存在,点C的坐标为
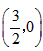 和
和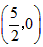
详解:①当
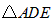 以点A为直角顶点时,作
以点A为直角顶点时,作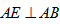 交x轴负半轴于点E,
交x轴负半轴于点E, ∵
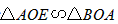
∴
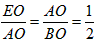
∵
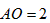
∴

∴点E坐标为(-1,0),
∴点C的坐标为
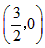
②当
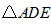 以点E为直角顶点时,同样有
以点E为直角顶点时,同样有
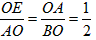
∴
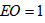
∴
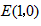
∴点C的坐标
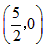 ,
,综合①②知满足条件的坐标有
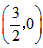 和
和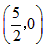 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,
(2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,

