题目内容
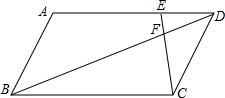如图，?ABCD的边AD上一点E，DE=| 1 | n |
1：（n+1）
1：（n+1）
．分析：首先证明△DEF∽△BCF，再利用相似三角形的性质得出
=
=
，即可得出DF：DB的比值．
| DE |
| BC |
| DF |
| BF |
| 1 |
| n |
解答：解：∵在?ABCD中，
∴AD∥BC，AD=BC，
∴△DEF∽△BCF，
∴
=
，
∵DE=
AD，
∴
=
=
，
∴DF：DB=1：（n+1）．
故答案为：1：（n+1）．
∴AD∥BC，AD=BC，
∴△DEF∽△BCF，
∴
| DE |
| BC |
| DF |
| BF |
∵DE=
| 1 |
| n |
∴
| DE |
| BC |
| DF |
| BF |
| 1 |
| n |
∴DF：DB=1：（n+1）．
故答案为：1：（n+1）．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出△DEF∽△BCF是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
如图正方形ABCD的边长为2cm，O是AB的中点，也是抛物线的顶点，OP⊥AB，两半圆的直径分别为OA与OB．抛物线经过C、D两点，且关于OP对称，则图中阴影部分的面积之和为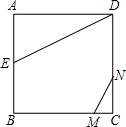
如图正方形ABCD的边长为2，AE=EB，线段MN的两端点分别在CB、CD上滑动，且MN=1，当CM为何值时△AED与以M、N、C为顶点的三角形相似？
（2011•泰宁县质检）如图菱形ABCD的边长为2，对角线BD=2，E、F分别是AD、CD上的两个动点，且满足AE+CF=2．
（2013•鄂州）如图正方形ABCD的边长为4，E、F分别为DC、BC中点．
如图正方形ABCD的边长是a，△AEF是等边三角形，点E在BC上，点F在CD上