题目内容
3.分式$\frac{1}{2x}$,$\frac{1}{2y2}$,$-\frac{1}{5xy}$的最简公分母为10xy2.分析 确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
解答 解:$\frac{1}{2x}$,$\frac{1}{2y2}$,$-\frac{1}{5xy}$分母分别是2x、2y2、5xy,故最简公分母是10xy2;
故答案是:10xy2.
点评 本题考查了最简公分母.通分的关键是准确求出各个分式中分母的最简公分母,确定最简公分母的方法一定要掌握.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
18.下列各式中正确的是( )
| A. | ${({\frac{{2{x^2}}}{2y}})^3}=\frac{{2{x^6}}}{{2{y^3}}}$ | B. | ${({\frac{2a}{a+b}})^2}=\frac{{4{a^2}}}{{{a^2}+{b^2}}}$ | ||
| C. | ${({\frac{m+n}{m-n}})^3}=\frac{{{{(m+n)}^3}}}{{{{(m-n)}^3}}}$ | D. | ${({\frac{x-y}{x+y}})^2}=\frac{{{x^2}-{y^2}}}{{{x^2}+{y^2}}}$ |
15.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)根据表中的数据,分别计算甲、乙两人的平均成绩:$\overline{x_甲}$=9环,$\overline{x_乙}$=9环.
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
| 甲 | 10 | 9 | 8 | 8 | 10 | 9 |
| 乙 | 10 | 10 | 8 | 10 | 7 | 9 |
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
12.“社会主义核心价值观”要求我们牢记心间,小明在“百度”搜索“社会主义核心价值观”,找到相关结果约为4280000个,数据4280000用科学记数法表示为( )
| A. | 0.428×107 | B. | 4.28×106 | C. | 4.28×105 | D. | 428×104 |
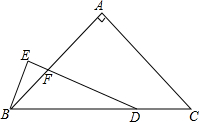 如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=$\frac{1}{2}$∠C,BE⊥DE于E,DE与AB交于点F,试探究线段BE与FD的数量关系,并证明.
如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=$\frac{1}{2}$∠C,BE⊥DE于E,DE与AB交于点F,试探究线段BE与FD的数量关系,并证明.