题目内容
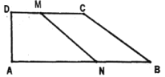
【题目】如图，在直角梯形ABCD中，DC∥AB，∠A=90°，AB=26cm，DC=18cm ，AD=4cm，动点M以1cm/s的速度从点D向点C运动，动点N从点B以2cm/s的速度向点A运动点M、N同时出发，当其中一个动点到达端点时停止运动，另一个动点也随之停止运动，设动点运动时间为t(s)，四边形ANMD的面积y(
)，y关于x的函数解析式并写出定义域_____.
【答案】y=-2t+52，0＜t＜13.
【解析】
要能根据函数图象的性质和图象上的数据，分析得出函数的类型和所需要的条件，结合实际意义即可求出定义域．
解：∵在直角梯形ABCD中，DC∥AB，∠A=90，
∴四边形ANMD也是直角梯形，因此它的面积为：
（DM+AN）×AD，
∵DM=t，AN=26-2t，AD= 4；
∴四边形AMND的面积：y=（t+26-2t）×4=-2t+52．
∵当其中一个动点到达端点停止运动时，另一个动点也随之停止运动；
∴当N点到达A点时，2t=26，
解得：t=13；
∴自变量t的取值范围是：0＜t＜13．
故答案为：0＜t＜13.
同步练习强化拓展系列答案
【题目】某市现在有两种用电收费方法：
分时电表 | 普通电表 | |
峰时（8:00～21:00） | 谷时（21:00到次日8:00） | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题：
（1）小明家庭某月用电总量为
千瓦·时（为常数）；谷时用电
千瓦·时，峰时用电
千瓦·时，分时计价时总价为
元，普通计价时总价为
元，求，与用电量的函数关系式.
（2）小明家庭使用分时电表是不是一定比普通电表合算呢？
（3）下表是路皓家最近两个月用电的收据：
谷时用电（千瓦·时） | 峰时用电（千瓦·时） |
181 | 239 |
根据上表，请问用分时电表是否合算？
