题目内容
等腰直角三角形ABC是⊙O的内接三角形，如果⊙O的半径为2cm，则△ABC的周长是________cm．
4
+4
分析：根据已知可得到AB是圆的直径，从而可求得AB的长；根据勾股定理可求AC的长，从而求周长．
解答：
解：∵等腰直角三角形ABC是⊙O的内接三角形，
∴AB为圆的直径，AB=4．
设AC=x，则x2+x2=16，
∴x=2．
∴△ABC的周长是2+2+4=4+4．
点评：本题考查的是圆周角定理及勾股定理的运用．
+4分析：根据已知可得到AB是圆的直径，从而可求得AB的长；根据勾股定理可求AC的长，从而求周长．
解答：
解：∵等腰直角三角形ABC是⊙O的内接三角形，∴AB为圆的直径，AB=4．
设AC=x，则x2+x2=16，
∴x=2
．∴△ABC的周长是2
+2+4=4+4．点评：本题考查的是圆周角定理及勾股定理的运用．
练习册系列答案
相关题目
把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点逆时针旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．
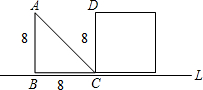AB与CD重合．设x秒时，三角形与正方形不重叠部分的面积为ym2．
如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．