题目内容
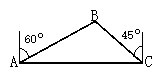
【题目】海船以5海里/小时的速度向正东方向行驶，在A处看见灯塔B在海船的北偏东60°方向，2小时后船行驶到C处，发现此时灯塔B在海船的北偏西45°方向，求此时灯塔B到C处的距离。
【答案】5(
)海里
【解析】本题考查的解直角三角形。对于60°和45°一般是放在直角三角形中所以需要做辅助线构造直角三角形。
解：如图，过B点作BD⊥AC于D,设BD=x (1分)
∴∠DAB＝90°-60°=30°,∠DCB＝90°-45°=45° (2分)
在Rt△ABD中，AD=xtan30°=
x （4分）
在Rt△BDC中BD=DC=x BC=
x (6分）
又AD＝5×2＝10 ∴x+x=10（7分） 得x=5(
) （8分）
∴BC=·5(
)=5(
)（海里） （9分）
答：灯塔B距C处5()海里
练习册系列答案
相关题目
