题目内容
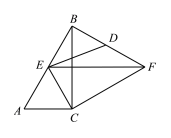
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△CEF,当E落在AB边上时,连接BF,取BF的中点D,连接ED,则ED的长是( )
A.2![]() B.4
B.4![]() C.6D.4
C.6D.4 ![]()
【答案】A
【解析】
先证明△ACE,△BCF是等边三角形,可求BD,BE的长,由勾股定理可求解.
解:∵∠ACB=90°,∠ABC=30°,AC=4,
∴∠A=90°![]() ∠ABC=60°,AB=8,BC=
∠ABC=60°,AB=8,BC=![]() ,
,
∵△ABC绕点C顺时针旋转得△CEF,
∴CA=CE,∠ACE=∠BCF,BC=CF,
∴△ACE是等边三角形,AE=AC=BE=EC=4,
∴∠BCF=∠ACE=60°,
∵CB=CF,
∴△BCF是等边三角形,
∴BF=BC=![]() ,∠CBF=60°,
,∠CBF=60°,
∵点D是BF中点,
∴BD=![]() ,且BE=4,∠ABF=90°,
,且BE=4,∠ABF=90°,
∴DE=![]() ;
;
故选:A.

练习册系列答案
相关题目