题目内容
15.计算:(1)23-17-(-7)+(-16)
(2)$\frac{2}{3}$+(-$\frac{1}{5}$)-1$+\frac{1}{3}$
(3)-15+6÷(-3)
(4)(-36)÷(-6)×$\frac{1}{6}$
(5)($\frac{1}{4}$$-\frac{1}{2}$+$\frac{1}{6}$)×24
(6)-34÷2$\frac{1}{4}$×(-$\frac{2}{3}$)2
(7)100÷(-2)2-(-2)÷(-$\frac{2}{3}$)
(8)101-103+105-107+…+197-199.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式结合后,相加即可得到结果;
(3)原式先计算除法运算,再计算加减运算即可得到结果;
(4)原式从左到右依次计算即可得到结果;
(5)原式利用乘法分配律计算即可得到结果;
(6)原式先计算乘方运算,再计算乘除运算即可得到结果;
(7)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(8)原式结合后,相加即可得到结果.
解答 解:(1)原式=23-17+7-16=30-33=-3;
(2)原式=$\frac{2}{3}$+$\frac{1}{3}$-$\frac{1}{5}$-1=-$\frac{1}{5}$;
(3)原式=-15-2=-17;
(4)原式=6×$\frac{1}{6}$=1;
(5)原式=6-12+4=-2;
(6)原式=-81×$\frac{4}{9}$×$\frac{4}{9}$=-16;
(7)原式=100÷4-2×$\frac{3}{2}$=25-3=22;
(8)原式=(101-103)+(105-107)+…+(197-199)=-2-2-…-2=-50.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.绝对值为4的数是( )
| A. | ±4 | B. | 4 | C. | -4 | D. | 2 |
4.根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个根x的范围是( )
| x | -2.1 | -2.2 | -2.3 | -2.4 | -2.5 |
| y=ax2+bx+c | -0.69 | -0.36 | -0.01 | 0.36 | 0.75 |
| A. | -2.2<x<-2.1 | B. | -2.4<x<-2.3 | C. | -2.3<x<-2.4 | D. | -2.4<x<-2.5 |
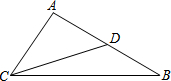 在△ABC中,D为AB的中点,连接CD.
在△ABC中,D为AB的中点,连接CD.