题目内容
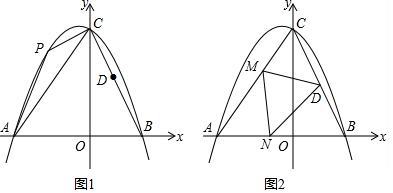
4.已知,△ABC在平面直角坐标系中的位置如图1所示,A点坐标为(-6,0),B点的坐标为(4,0),点D为BC的中点,经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.(1)求抛物线的解析式;
(2)点P为直线AC上方的抛物线上一动点,当点P运动到什么位置时,△APC的面积最大?求出此时P点的坐标和△APC的最大面积;
(3)已知M、N分别是线段AC、AB上的两个动点,点M由A以每秒1.2个单位向C出发,点N由B以每秒1个单位的速度向A运动,两点同时出发,当一个点停止运动时另一个点也停止运动,连接MN、DM、DN,问是否存在t使得DM平分∠CMN的同时DN也平分∠MNB?若存在,请直接写出t的值;若不存在,请说明理由.
分析 (1)利用待定系数法直接求出抛物线解析式;
(2)先利用面积最大这一特点确定出点P的坐标,再用三角形的面积之和即可得出结论;
(2)先判断出∠MDN=90°-$\frac{1}{2}$∠BAC,进而得出∠MDN=∠ABC=∠ACB,利用三角形的内角和即可得出∠CDM=∠DNM,进而判断出△CDM∽△BND,得出比例式,最后代入即可确定出时间.
解答 解:(1)∵经过点A(-6,0)、B(4,0)、C三点的抛物线的解析式为y=ax2+bx+8.
∴$\left\{\begin{array}{l}{36a-6b+8=0}\\{16a+4b+8=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8.
(2)∵抛物线的解析式为y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8②.
∴C(0,8),
∵A(-6,0),
∴直线AC解析式为y=$\frac{4}{3}$x+8,
∴作直线l,使l∥AC,设直线l解析式为y=$\frac{4}{3}$x+m①,
当直线l和抛物线只有一个交点时,△APC的面积最大,
联立①②化简得,x2+6x-(24-3m)=0,
∴△=36+4(24-3m)=0,
∴m=11,
∴x=-3,
∴P(-3,7),
如图1,
过点P作PE⊥AE于E,
∴AE=3,PE=7,OE=3,OC=8,
∵直线AC解析式为y=$\frac{4}{3}$x+8,
∴F(-3,4),
∴PF=PE-EF=3,
∴S△APC的最大=S△APF+S△CPF=$\frac{1}{2}$×PF×AE+$\frac{1}{2}$×PF×OE=$\frac{1}{2}$×PF×(AE+OE)=$\frac{1}{2}$×3×6=9.
即:P点的坐标为(-3,7),△APC的最大面积为9.
(3)如图,
∵DM平分∠CMN,
∴∠DMN=∠DMC=$\frac{1}{2}$∠CMN
∵DN也平分∠MNB,
∴∠DNB=∠DNM=$\frac{1}{2}$∠BNM,
在△AMN中,180°-∠BAC+∠CMN+∠BNM=360°,(三角形的外角和为360°)
∴∠CMN+∠BNM=180°+∠BAC
在△DMN中,∠MDN=180°-(∠DMN+∠DNM)
=180°-$\frac{1}{2}$(∠CMN+∠BNM)
=180°-$\frac{1}{2}$(180°+∠BAC)
=90°-$\frac{1}{2}$∠BAC.
∵A(-6,0),B(4,0),C(0,8),
∴AC=10,AB=10,BC=4$\sqrt{5}$
∴AB=AC,
连接AD,
∵点D是BC中点,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC,AD⊥BC
∴∠ABC=∠ACB=90°-$\frac{1}{2}$∠BAC,
∵∠MDN=90°-$\frac{1}{2}$∠BAC,
∴∠ABC=∠ACB=∠MDN,
∵∠DMN=∠DMC,
∴∠CDM=∠DNM,
∵∠DNB=∠DNM,
∴∠CDM=∠DNB,
∵∠ACB=∠ABC,
∴△CDM∽△BND,
∴$\frac{CD}{BN}=\frac{CM}{BD}$,
由运动知,BN=t,AM=1.2t,
∴CM=10-AM=10-1.2t,
∵点D是BC中点,且BC=4$\sqrt{5}$
∴CD=BD=$\frac{1}{2}$BC=2$\sqrt{5}$,
∴$\frac{2\sqrt{5}}{t}=\frac{10-1.2t}{2\sqrt{5}}$,
∴3t2-25t+50=0.
∴t=5或t=$\frac{10}{3}$.
点评 此题是二次函数综合题,主要考查了待定系数法,函数的极值,三角形的面积计算方法,三角形相似的判定和性质,角平分线的性质,三角形的内角和,解本题的关键是∠ABC=∠ACB=∠MDN,得出△CDM∽△BND,是解本题的难点,是一道较好的中考常考题.

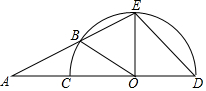 如图,CD是半圆的直径,O为圆心,E是半圆上一点,且∠EOD=93°,A是DC延长线上一点,AE与半圆相交于点B.若AB=OC,则∠EAD=31°,∠EOB=56°.
如图,CD是半圆的直径,O为圆心,E是半圆上一点,且∠EOD=93°,A是DC延长线上一点,AE与半圆相交于点B.若AB=OC,则∠EAD=31°,∠EOB=56°.
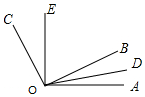 如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.
如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.