题目内容
在△ABC中，AB=8，AC=6，点D、E分别为AB，AC边上的点．且AD=3，则当AE= 时，△ABC与△ADE相似．
考点：相似三角形的判定
专题：
分析：题中没有指明具体的对应边，故应该分两种情况进行分析，分别是△ABC∽△ADE或△ABC∽△AED．
解答：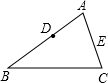
解：∵△ABC与△ADE相似
∴△ABC∽△ADE或△ABC∽△AED
①当△ABC∽△ADE时：
则
=
，即
=
，
解得AE=
；
②当△ABC∽△AED时：
则
=
，即
=
，
解得AE=4
∴当AE=
或4时，△ABC与△ADE相似．
故答案为：
或4．
解：∵△ABC与△ADE相似∴△ABC∽△ADE或△ABC∽△AED
①当△ABC∽△ADE时：
则
| AB |
| AC |
| AD |
| AE |
| 8 |
| 6 |
| 3 |
| AE |
解得AE=
| 9 |
| 4 |
②当△ABC∽△AED时：
则
| AB |
| AE |
| AC |
| AD |
| 8 |
| AE |
| 6 |
| 3 |
解得AE=4
∴当AE=
| 9 |
| 4 |
故答案为：
| 9 |
| 4 |
点评：此题考查了相似三角形的性质．此题难度适中，注意掌握分类讨论思想与数形结合思想的应用．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
看图填空．