题目内容
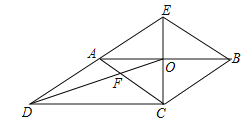
【题目】如图,线段AB为⊙O的直径,点C,E在⊙O上,![]() ,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
(1)求证:CF=BF;
(2)若cos∠ABE![]() ,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.
,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)延长CD交⊙O于G,如图,利用垂径定理得到![]() ,则可证明
,则可证明![]() ,然后根据圆周角定理得∠CBE=∠GCB,从而得到CF=BF ;
,然后根据圆周角定理得∠CBE=∠GCB,从而得到CF=BF ;
(2)连接OC交BE于H,如图,先利用垂径定理得到OC⊥BE ,再在Rt△OBH中利用解直角三角形得到BH![]() ,OH
,OH![]() ,接着证明△OHB∽△OCM得到∠OCM=∠OHB=90°,然后根据切线的判定定理得到结论.
,接着证明△OHB∽△OCM得到∠OCM=∠OHB=90°,然后根据切线的判定定理得到结论.
(1)延长CD交⊙O于G,如图,
∵CD⊥AB,∴![]() ,
,
![]() ,∴
,∴![]() ,
,
∴∠CBE=∠GCB,
∴CF=BF;
(2)连接OC交BE于H,如图,
∵![]() ,∴OC⊥BE,
,∴OC⊥BE,
在Rt△OBH中,cos∠OBH![]() ,
,
∴BH![]() ,
,
∴OH![]()
![]() ,
,
∴![]() ,而∠HOB=∠COM,
,而∠HOB=∠COM,
∴△OHB∽△OCM,
∴∠OCM=∠OHB=90°,
∴OC⊥CM,
∴直线CM是⊙O的切线.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目