题目内容
如图，抛物线
经过
、
两点，与
轴交于另一点
．
（1）求抛物线的解析式；
（2）已知点
在第一象限的抛物线上，求点
关于直线
对称的点的坐标；
（3）在（2）的条件下，连接
，点
为抛物线上一点，且
，求点的坐标．
解：（1）
抛物线经过，两点，
解得
抛物线的解析式为
．
（2）点在抛物线上，
，
即
，
或
．
点在第一象限，点的坐标为
．
由（1）知
．
设点关于直线的对称点为点
．
，
，且
，
，
点在
轴上，且
．
，
．
即点关于直线对称的点的坐标为（0，1）．
（3）方法一：作
于
，
于．
由（1）有：
，
．
，
且．
，
．
，
，
，
．
设
，则
，
，
．
点在抛物线上，
，
（舍去）或
，
．
方法二：过点作的垂线交直线
于点
，过点作
轴于
．过点作
于
．
．
，
又
，
．
，
，
．
由（2）知
，
．
，直线
的解析式为
．
解方程组
得
点的坐标为
．
练习册系列答案
相关题目
（2013•高要市二模）已知：如图，抛物线经过点O、A、B三点，四边形OABC是直角梯形，其中点A在x轴上，点C在y轴上，BC∥OA，A（12，0）、B（4，8）．
（2012•邯郸一模）已知：如图，抛物线y=-x2+bx+c的图象经过点A（1，0），B （0，5）两点，该抛物线与x轴的另一交点为C．
经过直线y=x－3与坐标轴的两个交点A、B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．
的点P的坐标．
如图，抛物线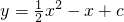
经过点A（0，
），直线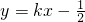
交抛物线于点P（点P不与点A重合）．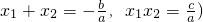
经过点P
，且与抛物线
相交于A，B两点。
与x轴分别交于M，N两点（点M在点N的左边），
与x轴分别交于E，F两点（点E在点F的左边），观察M，N，E，F四点的坐标，写出一条正确的结论，并通过计算说明；