题目内容
 如图,在△ABC中,若点P是∠ABC与∠ACB的外角平分线的交点.
如图,在△ABC中,若点P是∠ABC与∠ACB的外角平分线的交点.(1)∠A=40°,则∠BPC=
(2)∠A=60°,则∠BPC=
(3)∠A=α,猜想∠BPC的大小,并证明你的猜想.
考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:先根据交平分线定义得到∠1=∠2,∠3=∠4,再利用三角形外角性质得∠BCP=∠A+∠ABC,即∠1+∠2=∠A+180°-∠3-∠4,变形为∠A=180°-2∠1-2∠3,接着根据三角形内角和定理得到∠BPC=180°-∠1-∠3,利用等式的性质易得∠BPC=90°+
∠A;
(1)把∠A=40°代入∠BPC=90°+
∠A计算即可;
(2)把∠A=60°代入∠BPC=90°+
∠A计算即可;
(3)把∠A=α代入∠BPC=90°+
∠A即可.
| 1 |
| 2 |
(1)把∠A=40°代入∠BPC=90°+
| 1 |
| 2 |
(2)把∠A=60°代入∠BPC=90°+
| 1 |
| 2 |
(3)把∠A=α代入∠BPC=90°+
| 1 |
| 2 |
解答:解: ∵点P是∠ABC与∠ACB的外角平分线的交点,
∵点P是∠ABC与∠ACB的外角平分线的交点,
∴∠1=∠2,∠3=∠4,
∵∠BCP=∠A+∠ABC,
∴∠1+∠2=∠A+180°-∠3-∠4
∴∠A=180°-2∠1-2∠3,
而∠BPC=180°-∠1-∠3,
∴2∠BPC-∠A=180°,
∴∠BPC=90°+
∠A;
(1)当∠A=40°,∠BPC=90°+
×40°=110°;
(2)当∠A=60°,∠BPC=90°+
×60°=120°;
(3)当∠A=α,∠BPC=90°+
α.
故答案为110°,120°.
 ∵点P是∠ABC与∠ACB的外角平分线的交点,
∵点P是∠ABC与∠ACB的外角平分线的交点,∴∠1=∠2,∠3=∠4,
∵∠BCP=∠A+∠ABC,
∴∠1+∠2=∠A+180°-∠3-∠4
∴∠A=180°-2∠1-2∠3,
而∠BPC=180°-∠1-∠3,
∴2∠BPC-∠A=180°,
∴∠BPC=90°+
| 1 |
| 2 |
(1)当∠A=40°,∠BPC=90°+
| 1 |
| 2 |
(2)当∠A=60°,∠BPC=90°+
| 1 |
| 2 |
(3)当∠A=α,∠BPC=90°+
| 1 |
| 2 |
故答案为110°,120°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形的外角性质.

练习册系列答案
相关题目
 如图,在△ABC中,过点C作CD∥AB,且∠1=70°,点E是AC边上的一点,且∠EFB=130°,∠2=20°,请你猜想直线EF与CD有怎样的位置关系,并说明理由.
如图,在△ABC中,过点C作CD∥AB,且∠1=70°,点E是AC边上的一点,且∠EFB=130°,∠2=20°,请你猜想直线EF与CD有怎样的位置关系,并说明理由. 如图,在长为a、宽为b的长方形场地中,横向有两条宽均为n的长方形草坪,斜向有一条平行四边形的草坪,且其中一边长为m,则图中空地面积用含有a、b、m、n的代数式表示是
如图,在长为a、宽为b的长方形场地中,横向有两条宽均为n的长方形草坪,斜向有一条平行四边形的草坪,且其中一边长为m,则图中空地面积用含有a、b、m、n的代数式表示是 已知,在平面直角坐标系xOy中,点A(1,0),B(3,0),点C为一动点.
已知,在平面直角坐标系xOy中,点A(1,0),B(3,0),点C为一动点.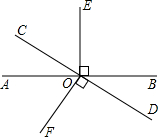 如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.