题目内容
 14、如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),如果要使△ABD与△ABC全等,且点D坐标在第四象限,那么点D的坐标是
14、如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),如果要使△ABD与△ABC全等,且点D坐标在第四象限,那么点D的坐标是(5,-1)
.分析:根据全等三角形的性质,三条对应边均相等,又顶点C与顶点D相对应,所以点D与C关于AB对称,即点D与点C对与AB的相对位置一样.
解答:解:∵△ABD与△ABC全等,
∴C、D关于AB对称,顶点C与顶点D相对应,即C点和D点到AB的相对位置一样.
∵由图可知,AB平行于x轴,
∴D点的横坐标与C的横坐标一样,即D点的横坐标为5.
又∵点A的坐标为(0,2),点C的坐标为(5,5),点D在第四象限,
∴C点到AB的距离为3.
∵C、D关于AB轴对称,
∴D点到AB的距离也为3,
∴D的纵坐标为-1.
故D(5,-1).
∴C、D关于AB对称,顶点C与顶点D相对应,即C点和D点到AB的相对位置一样.
∵由图可知,AB平行于x轴,
∴D点的横坐标与C的横坐标一样,即D点的横坐标为5.
又∵点A的坐标为(0,2),点C的坐标为(5,5),点D在第四象限,
∴C点到AB的距离为3.
∵C、D关于AB轴对称,
∴D点到AB的距离也为3,
∴D的纵坐标为-1.
故D(5,-1).
点评:此题考查的是点关于轴对称的有关知识,合理的数形结合可以使问题简单明了.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
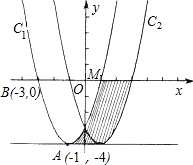 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)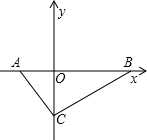 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=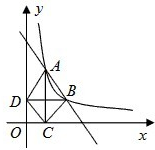 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是