题目内容
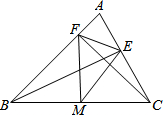 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10,EF=4.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10,EF=4.(1)求△MEF的周长;
(2)若∠ABC=50°,∠ACB=60°,求△EFM的三个内角的度数.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半求出EM、FM,再根据三角形的周长的定义列式计算即可得解;
(2)根据等腰三角形两底角相等求出∠BMF,∠CME,然后根据平角等于180°列式计算即可求出∠EMF,再根据等腰三角形两底角相等求出另两个角即可.
(2)根据等腰三角形两底角相等求出∠BMF,∠CME,然后根据平角等于180°列式计算即可求出∠EMF,再根据等腰三角形两底角相等求出另两个角即可.
解答:
解:(1)∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=
BC=5,
FM=
BC=5,
∴△MEF周长=EF+EM+FM=4+5+5=14;
(2)∵BM=FM,∠ABC=50°,
∴∠MBF=∠MFB=50°,
∴∠BMF=180°-2×50°=80°,
∵CM=EM,∠ACB=60°,
∴∠MCE=∠MEC=60°,
∴∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°,
∴∠MEF=∠MFE=
(180°-∠EMF)=70°,
∴△MEF的三个内角分别为40°、70°、70°.
∴EM=
| 1 |
| 2 |
FM=
| 1 |
| 2 |
∴△MEF周长=EF+EM+FM=4+5+5=14;
(2)∵BM=FM,∠ABC=50°,
∴∠MBF=∠MFB=50°,
∴∠BMF=180°-2×50°=80°,
∵CM=EM,∠ACB=60°,
∴∠MCE=∠MEC=60°,
∴∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°,
∴∠MEF=∠MFE=
| 1 |
| 2 |
∴△MEF的三个内角分别为40°、70°、70°.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,平角的定义,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
下列各式与-
相加的结果可以用一个二次根式表示的是( )
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
 如图,已知AD∥BC,∠B=40°,DB平分∠ADE,则∠DEC为( )
如图,已知AD∥BC,∠B=40°,DB平分∠ADE,则∠DEC为( )| A、40° | B、60° |
| C、70° | D、80° |
下列长度的三条线段,能组成三角形的是( )
| A、2cm,3cm,4cm |
| B、1cm,4cm,2cm |
| C、1cm,2cm,3cm |
| D、6cm,2cm,3cm |
一元二次方程x(x-7)=0的根是( )
| A、0 | B、7 | C、0和7 | D、0和-7 |
一元二次方程3x2-2x=0的解( )
A、x1=0,x2=
| ||
B、x1=0,x2=-
| ||
C、x1=0,x2=
| ||
D、x1=0,x2=-
|