题目内容
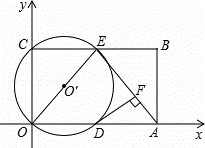
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)由已知可得,△ AOE是等腰三角形.那么直线BC
AOE是等腰三角形.那么直线BC
上存不存在除点E以外的点P,使△AOP也是等腰三角
形?如果不存在,说明理由;如果存在,直接写出P点
的坐标.
 |
(1)解:在矩形OABC中,设OC=x,则OA=x+2,
∴x(x+2)=15,
∴x1=3,x2=﹣5,
∴x2=﹣5(不合题意,舍去),
∴OC=3,OA=5;
(2)证明:如图1,连接O′D,

在矩形OABC中,OC=AB,∠OCB=∠ABC=90°,CE=BE= ,
,
在△OCE和△ABE中,
 ,
,
∴△0CE≌△ABE(SAS),
∴EA=EO,
∴∠1=∠2;
∵在⊙O′中,O′O=O′D,
∴∠1=∠3,
∴∠3=∠2,
∴O′D∥AE;
∵DF⊥AE,
∴DF⊥O′D,
∵点D在⊙O′上,O′D为⊙O′的半径,
∴DF为⊙O′切线;
(3)解:存在.
其坐标为(1,3)或(9,3)或(4,3)或(﹣4,3).

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 -5=0 D.x2-1=0
-5=0 D.x2-1=0





 =
=  B.
B. C.∠B=∠D D.∠C=∠AED
C.∠B=∠D D.∠C=∠AED ,其图象在第一、第三象限内,则k的值可为 .(写出满足条件的一个k的值即可).
,其图象在第一、第三象限内,则k的值可为 .(写出满足条件的一个k的值即可).