题目内容
 如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
分析:(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
解答:证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
∴∠A=∠B,
在△ACD和△BEC中
|
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
点评:本题考查了平行线性质,全等三角形的性质和判定,等腰三角形性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目

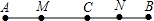
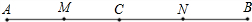
 (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长; 如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=
如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=