题目内容
以后我们会知道：在Rt△ABC中，∠C=90°，若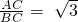
，则∠B=60°；现在已知关于x的一次函
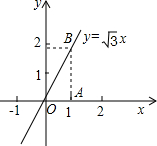数
．
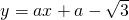（1）当a取不同的非0实数时，我们可以得到一系列的一次函数，这些函数都过一个共同点P，请求P的坐标；
（2）当a为何值时这个一次函数是正比例函数？
（3）当这个一次函数是正比例函数时，它的图象与x轴的夹角a（a取锐角）．
解：（1）当a取不同的非0实数时，这些函数都过（-1，-
）点，P的坐标是（-1，-）；
（2）由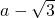
=0可得当a=时这个一次函数是正比例函数；
（3）∵当这个一次函数是正比例函数时，它的解析式是y=x，
∴tan∠AOB=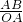
=；
∴∠AOB=60°；
∴它的图象与x轴的夹角a是60°．
分析：（1）把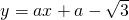变形为
后可得出这些函数都过的点的坐标是；
（2）由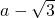=0可得出当a为何值时这个一次函数是正比例函数；
（3）根据正比例函数的解析式求出tan∠AOB的值即可得出它的图象与x轴的夹角a．
点评：此题考查了一次函数的综合应用，关键是对给出的一次函数的解析式进行变形，求出a的值，再利用正比例函数的解析式求角的度数．
）点，P的坐标是（-1，-）；（2）由
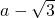=0可得当a=时这个一次函数是正比例函数；（3）∵当这个一次函数是正比例函数时，它的解析式是y=
x，∴tan∠AOB=
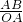=；∴∠AOB=60°；
∴它的图象与x轴的夹角a是60°．
分析：（1）把
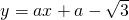变形为后可得出这些函数都过的点的坐标是；（2）由
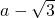=0可得出当a为何值时这个一次函数是正比例函数；（3）根据正比例函数的解析式求出tan∠AOB的值即可得出它的图象与x轴的夹角a．
点评：此题考查了一次函数的综合应用，关键是对给出的一次函数的解析式进行变形，求出a的值，再利用正比例函数的解析式求角的度数．
练习册系列答案
相关题目
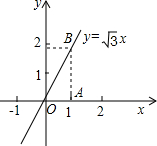数