题目内容
 已知两个反比例函数y=
已知两个反比例函数y=| k |
| x |
| 6 |
| x |
| 6 |
| x |
| k |
| x |
(1)求证:△ODB与△OCA的面积相等;
(2)记S=S△OAB-S△PAB,当k变化时,求S的最大值,并求当S取最大值时△OAB的面积.
分析:(1)直接根据反比例函数系数k的几何意义进行解答即可;
(2)设出P点坐标,进而可得出A、B两点坐标,由反比例函数系数k的几何意义可知S=S△OAB-S△PAB=S△四边形PBOA-2S△PAB,再把A、B、P三点的坐标代入即可.
(2)设出P点坐标,进而可得出A、B两点坐标,由反比例函数系数k的几何意义可知S=S△OAB-S△PAB=S△四边形PBOA-2S△PAB,再把A、B、P三点的坐标代入即可.
解答: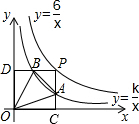 解:(1)∵点AB均是反比例函数y=
解:(1)∵点AB均是反比例函数y=
(k>0)上的点,PC⊥x轴,PD⊥y轴,
∴S△ODB=S△OCA=
,即△ODB与△OCA的面积相等;
(2)设P(x,
),则A(x,
),B(k,
),
∵点P在反比例函数y=
的图象上,
∴S矩形PDOC=6,
∵S△ODB=S△OCA=
,
∴S四边形PBOA=S矩形PDOC-(S△ODB+S△OCA)=6-k,
∴S=S△OAB-S△PAB=S△四边形PBOA-2S△PAB=6-k-2×
(
-
)(x-
)=k-
,
∴当k=
时S有最大值,S最大=
-
=
;
当k=
时,S△PAB=
(
-
)(x-
)=
,
∴S△OAB=S+S△PAB=
+
=
.
 解:(1)∵点AB均是反比例函数y=
解:(1)∵点AB均是反比例函数y=| k |
| x |
∴S△ODB=S△OCA=
| k |
| 2 |
(2)设P(x,
| 6 |
| x |
| k |
| x |
| 6 |
| x |
∵点P在反比例函数y=
| 6 |
| x |
∴S矩形PDOC=6,
∵S△ODB=S△OCA=
| k |
| 2 |
∴S四边形PBOA=S矩形PDOC-(S△ODB+S△OCA)=6-k,
∴S=S△OAB-S△PAB=S△四边形PBOA-2S△PAB=6-k-2×
| 1 |
| 2 |
| 6 |
| x |
| k |
| x |
| kx |
| 6 |
| k2 |
| 6 |
∴当k=
| 3 |
| 2 |
| 3 |
| 2 |
(
| ||
| 6 |
| 9 |
| 8 |
当k=
| 3 |
| 2 |
| 1 |
| 2 |
| 6 |
| x |
| k |
| x |
| kx |
| 6 |
| 29 |
| 32 |
∴S△OAB=S+S△PAB=
| 9 |
| 8 |
| 29 |
| 32 |
| 65 |
| 32 |
点评:本题考查的是反比例函数综合题,树脂反比例函数系数k的几何意义是解答此题的关键.

练习册系列答案
相关题目
 已知两个反比例函数
已知两个反比例函数
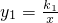 和
和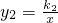 (k1>k2>0)在平面直角坐标系xOy第一象限内的图象如图所示,动点A在
(k1>k2>0)在平面直角坐标系xOy第一象限内的图象如图所示,动点A在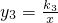 ,动点N在y3上,若∠AON=90°,求
,动点N在y3上,若∠AON=90°,求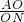 的值.
的值.
 已知两个反比例函数y=
已知两个反比例函数y= (k>0)和y=
(k>0)和y= 在第一象限内的图象如图所示,点P是y=
在第一象限内的图象如图所示,点P是y=