题目内容
 如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上.
如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上.
求证:△ACB∽△DCE.
证明:由图可知,BC⊥AE于点C.
∴∠ACB=∠DCE=90°.
在△ABC和△DEC中,
 =
=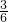 =
= ,
,
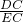 =
= =
= ,
,
∴ .
.
∴△ACB∽△DCE.
分析:根据BC⊥AE于点C,得出∠ACB=∠DCE=90°.再根据网格中的每个小正方形的边长都是1,求出 .然后即可求证
.然后即可求证
△ABD∽△DEC.
点评:此题考查学生对相似三角形的判定这一知识点的理解与掌握,解得此题的关键是求出 .这是此题的突破点.
.这是此题的突破点.
∴∠ACB=∠DCE=90°.
在△ABC和△DEC中,
 =
=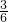 =
= ,
,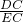 =
= =
= ,
,∴
 .
.∴△ACB∽△DCE.
分析:根据BC⊥AE于点C,得出∠ACB=∠DCE=90°.再根据网格中的每个小正方形的边长都是1,求出
 .然后即可求证
.然后即可求证△ABD∽△DEC.
点评:此题考查学生对相似三角形的判定这一知识点的理解与掌握,解得此题的关键是求出
 .这是此题的突破点.
.这是此题的突破点. 
练习册系列答案
相关题目
 18、已知:如图,网格中的每个小正方形的边长都是1个单位,请在图中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
18、已知:如图,网格中的每个小正方形的边长都是1个单位,请在图中画出一个与格点△DEF相似但相似比不等于1的格点三角形. 如图,网格中的每个小正方形的边长为1,如果把阴影部分剪拼成一个正方形,那么这个新正方形的边长是
如图,网格中的每个小正方形的边长为1,如果把阴影部分剪拼成一个正方形,那么这个新正方形的边长是 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( ) 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是
小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是 如图,网格中的每个小正方形的边长为1,如果把阴影部分剪拼成一个正方形,那么这个新正方形的边长是 ( )
如图,网格中的每个小正方形的边长为1,如果把阴影部分剪拼成一个正方形,那么这个新正方形的边长是 ( )