题目内容
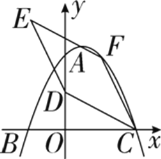
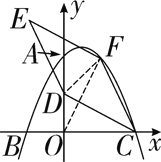
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
【答案】(1) y=-![]() x2+x+8,C (8,0);(2) ①50;②18.
x2+x+8,C (8,0);(2) ①50;②18.
【解析】
(1)把A点和B点坐标代入y=-![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
(2)①连结DF,OF,如图,设F(t,-![]() t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=-t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=-t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t-8,-![]() t2+t+12),然后把E(t-8,-
t2+t+12),然后把E(t-8,-![]() t2+t+12)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
t2+t+12)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
解:(1)∵二次函数y=-![]() x2+Bx+C过A(0,8)、B(-4,0)两点,
x2+Bx+C过A(0,8)、B(-4,0)两点,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的解析式为y=-![]() x2+x+8,
x2+x+8,
当y=0时,解得x1=-4,x2=8,
∴C点坐标为(8,0);
(2)①如解图,连接DF,OF,设F(M,-![]() M2+M+8),
M2+M+8),
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF-S△OCD,
=![]() ×4×M+
×4×M+![]() ×8×(-
×8×(-![]() M2+M+8)-
M2+M+8)-![]() ×8×4
×8×4
=2M-M2+4M+32-16
=-M2+6M+16
=-(M-3)2+25,
当M=3时,△CDF的面积有最大值,最大值为25,
∵四边形CDEF为平行四边形,
∴S四边形CDEF=2S△CDF=50,
∴S的最大值为50;
②S=18.
∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF,
∵点C向左平移8个单位,再向上平移4个单位得到点D,
∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(M-8,-![]() M2+M+12),
M2+M+12),
∵E(M-8,-![]() M2+M+12)在抛物线上,
M2+M+12)在抛物线上,
∴-![]() (M-8)2+(M-8)+8=-
(M-8)2+(M-8)+8=-![]() M2+M+12,
M2+M+12,
解得M=7,
当M=7时,S△CDF=-(7-3)2+25=9,
∴此时S=2S△CDF=18.

 特高级教师点拨系列答案
特高级教师点拨系列答案