题目内容
【题目】已知点![]() 在抛物线
在抛物线![]() 上.
上.
(1)求抛物线的解析式;
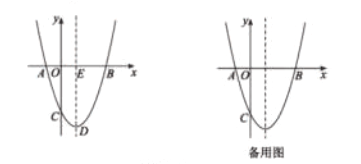
(2)如图1,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,设抛物线与
,设抛物线与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() ,求证
,求证![]() ;
;
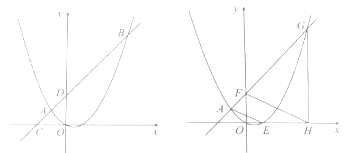
(3)如图2,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() 两点,点
两点,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向匀速运动,速度为每秒
方向匀速运动,速度为每秒![]() 个单位长度,同时点
个单位长度,同时点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向匀速运动,速度为每秒1个单位长度,点
轴正方向匀速运动,速度为每秒1个单位长度,点![]() 是直线
是直线![]() 与抛物线的一个交点,当运动到
与抛物线的一个交点,当运动到![]() 秒时,
秒时,![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)抛物线的解析式为:y=![]() x2-
x2-![]() x;(2)证明见解析;(3)
x;(2)证明见解析;(3)![]() ;
;![]() .
.
【解析】
试题分析:(1)把A,B两点坐标代入![]() ,解方程组求出a,b的值,即可得到二次函数解析式;
,解方程组求出a,b的值,即可得到二次函数解析式;
(2)过点A作AN⊥x轴于点N,则N(-1,0),再求出E点坐标,从而可求tan∠AEN=![]() ,再求出直线AF的解析式与抛物线方程联立,求出点G的坐标,则可得到tan∠FHO=
,再求出直线AF的解析式与抛物线方程联立,求出点G的坐标,则可得到tan∠FHO=![]() ,从而得证;
,从而得证;
(3)进行分类讨论 即可得解.
试题解析:(1)∵点A(-1,1),B(4,6)在抛物线y=ax2+bx上
∴a-b=1,16a+4b=6
解得:a=![]() ,b=-
,b=-![]()
∴抛物线的解析式为:y=![]() x2-
x2-![]() x
x
(2)过点A作AN⊥x轴于点N,则N(-1,0)
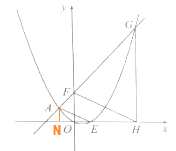
∴AN=1
当y=0时,![]() x2-
x2-![]() x=0
x=0
解得:x=0或1
∴E(1,0)
∴EN=2
∴tan∠AEN=![]()
设直线AF的解析式为y=kx+m
∵A (-1,1)在直线AF上,
∴-k+m=1
即:k=m-1
∴直线AF的解析式可化为:y=(m-1)x+m
与y=![]() x2-
x2-![]() x联立,得(m-1)x+m=
x联立,得(m-1)x+m=![]() x2-
x2-![]() x
x
∴(x+1)(x-2m)=0
∴x=-1或2m
∴点G的横坐标为2m
∴OH=2m
∵OF=m
∴tan∠FHO=![]()
∴∠AEN=∠FHO
∴FH∥AE
(3)![]() ;
;![]() .
.

练习册系列答案
相关题目