题目内容
如图,抛物线:![]() 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),

1.求此抛物线的关系式;并直接写出点A、B的坐标
2.求过A、B、C三点的圆的半径.
3.在抛物线上找点P,在y轴上找点E,使以A、B、P、E为顶点的四边形是平行四边形,求点P、E的坐标.
1.A(﹣1,0)、B(3,0)
2.2
3.见解析
解析:(1)∵抛物线y=![]() x2+bx+c的顶点为C(1,﹣2),
x2+bx+c的顶点为C(1,﹣2),
∴﹣ =﹣
=﹣![]() =1,解得b=﹣1,
=1,解得b=﹣1, =
= =﹣2,解得c=﹣
=﹣2,解得c=﹣ ,
,
∴抛物线解析式为y=![]() x2﹣x﹣
x2﹣x﹣![]() ,令y=0,则
,令y=0,则![]() x2﹣x﹣
x2﹣x﹣![]() =0,解得x1=﹣1,x2=3,∴点A、B的坐标为:A(﹣1,0)、B(3,0);
=0,解得x1=﹣1,x2=3,∴点A、B的坐标为:A(﹣1,0)、B(3,0);
(2)∵A(﹣1,0)、B(3,0)、C(1,﹣2),∴AB=3﹣(﹣1)=4,AC=![]() =2
=2![]() ,
,
BC=![]() =2
=2![]() ,
,
∴AB2=16,AC2+BC2=8+8=16,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,AB是直径,
故半径为2;
(3)①当AB是平行四边形的边时,PE=AB=4,且点P、E的纵坐标相等,
∴点P的横坐标为4或﹣4,
∴y=![]() ×42﹣4﹣
×42﹣4﹣![]() =
=![]() ,
,
或y=![]() ×42+4﹣
×42+4﹣![]() =
=![]() ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),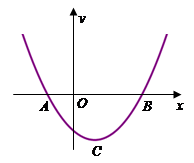
 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),
 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.