题目内容
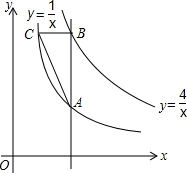 如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数
如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数 的图象于点A,交函数
的图象于点A,交函数 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交 于点c,边接AC.
于点c,边接AC.
(1)当点P的坐标为(1,0)时,求△ABC的面积;
(2)当点P的坐标为(1,0)时,在y轴上是否存在一点Q,使A、O、Q三点为顶点的三角形△QAO为等腰三角形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
(3)请你连接OA和OC.当点P的坐标为(t,0)时,△OAC的面积是否随t的值的变化而变化?请说明理由.
解:(1)当当点P的坐标为(1,0)时,点A、B的横坐标为1,
∵点A在反比例函数y= 上,点B在反比例函数y=
上,点B在反比例函数y= 上,
上,
∴点A(1,1),点B(1,4),
∵BC∥x轴,
∴点C的纵坐标为4,
又∵点C在y= 上,
上,
∴点C的坐标为( ,4),
,4),
∴AB=3,BC= ,
,
∴S△ABC= ×BC×AB=
×BC×AB= ;
;
(2)如图①所示:OA= =
= ,
,
①若OA=OP,点P位于P1或P2位置,此时P1(0,- ),P2(0,
),P2(0, );
);
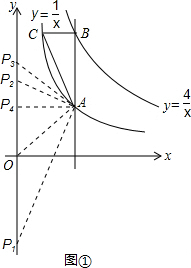
②若AP=AO,点P位于P3位置,此时P3(0,2);
③若PO=PA,点P位于P4位置,此时P4(0,1);
(3)过点C作CE⊥x轴于点E,CD⊥y轴于点D,如图②所示:
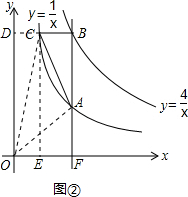
∵点P的坐标为(t,0),
∴点A的坐标为(t, ),点B(t,
),点B(t, ),点C(
),点C( ,
, ),
),
∴S△OAC=S矩形CDOE+S梯形AFEC-S△OCD-S△OAF=1+ (
( +
+ )×(t-
)×(t- )-
)- -
- =
= ;
;
故△OAC的面积不随t的值的变化而变化.
分析:(1)当点P的坐标为(1,0)时,点A、B的横坐标为1,分别代入解析式,求出A、B的坐标,由点B的坐标可得点C的纵坐标,代入y= ,可得点C的坐标,表示出BC、AB的长度后,即可得出△ABC的面积.
,可得点C的坐标,表示出BC、AB的长度后,即可得出△ABC的面积.
(2)先求出OA的长度,然后分情况讨论,①OA=OP,②AP=AO,③PO=PA,分别得出点Q的坐标即可.
(3)根据题意可得点A的坐标为(t, ),点B(t,
),点B(t, ),点C(
),点C( ,
, ),过点C作CE⊥x轴于点E,CD⊥y轴于点D,根据S△OAC=S矩形CDOE+S梯形AFEC-S△OCD-S△OAF,表示出示出△OAC的面积,即可得出答案.
),过点C作CE⊥x轴于点E,CD⊥y轴于点D,根据S△OAC=S矩形CDOE+S梯形AFEC-S△OCD-S△OAF,表示出示出△OAC的面积,即可得出答案.
点评:本题考查了反比例函数的综合,涉及了反比例函数的k的几何意义,梯形的面积及等腰三角形的判定,解答本题的关键是分类讨论思想及数形结合思想的综合运用,难度较大.
∵点A在反比例函数y=
 上,点B在反比例函数y=
上,点B在反比例函数y= 上,
上,∴点A(1,1),点B(1,4),
∵BC∥x轴,
∴点C的纵坐标为4,
又∵点C在y=
 上,
上,∴点C的坐标为(
 ,4),
,4),∴AB=3,BC=
 ,
,∴S△ABC=
 ×BC×AB=
×BC×AB= ;
;(2)如图①所示:OA=
 =
= ,
,①若OA=OP,点P位于P1或P2位置,此时P1(0,-
 ),P2(0,
),P2(0, );
);
②若AP=AO,点P位于P3位置,此时P3(0,2);
③若PO=PA,点P位于P4位置,此时P4(0,1);
(3)过点C作CE⊥x轴于点E,CD⊥y轴于点D,如图②所示:

∵点P的坐标为(t,0),
∴点A的坐标为(t,
 ),点B(t,
),点B(t, ),点C(
),点C( ,
, ),
),∴S△OAC=S矩形CDOE+S梯形AFEC-S△OCD-S△OAF=1+
 (
( +
+ )×(t-
)×(t- )-
)- -
- =
= ;
;故△OAC的面积不随t的值的变化而变化.
分析:(1)当点P的坐标为(1,0)时,点A、B的横坐标为1,分别代入解析式,求出A、B的坐标,由点B的坐标可得点C的纵坐标,代入y=
 ,可得点C的坐标,表示出BC、AB的长度后,即可得出△ABC的面积.
,可得点C的坐标,表示出BC、AB的长度后,即可得出△ABC的面积.(2)先求出OA的长度,然后分情况讨论,①OA=OP,②AP=AO,③PO=PA,分别得出点Q的坐标即可.
(3)根据题意可得点A的坐标为(t,
 ),点B(t,
),点B(t, ),点C(
),点C( ,
, ),过点C作CE⊥x轴于点E,CD⊥y轴于点D,根据S△OAC=S矩形CDOE+S梯形AFEC-S△OCD-S△OAF,表示出示出△OAC的面积,即可得出答案.
),过点C作CE⊥x轴于点E,CD⊥y轴于点D,根据S△OAC=S矩形CDOE+S梯形AFEC-S△OCD-S△OAF,表示出示出△OAC的面积,即可得出答案.点评:本题考查了反比例函数的综合,涉及了反比例函数的k的几何意义,梯形的面积及等腰三角形的判定,解答本题的关键是分类讨论思想及数形结合思想的综合运用,难度较大.

练习册系列答案
相关题目
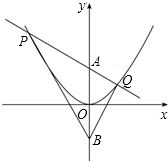 于P,Q两点.
于P,Q两点.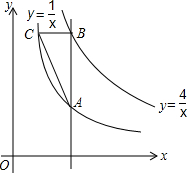 如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数
如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数 如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数y=
如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数y=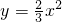
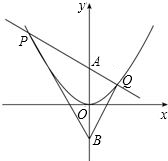 于P,Q两点.
于P,Q两点.