题目内容
如图,点A为y轴正半轴上一点,A,B两点关于x轴对称,过点A任作直线交抛物线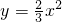
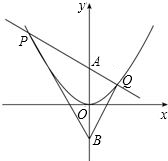 于P,Q两点.
于P,Q两点.
(1)求证:∠ABP=∠ABQ;
(2)若点A的坐标为(0,1),且∠PBQ=60°,试求所有满足条件的直线PQ的函数解析式.
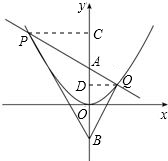
(1)证明:如图,分别过点P,Q作y轴的垂线,垂足分别为C,D.
设点A的坐标为(0,t),则点B的坐标为(0,-t).
设直线PQ的函数解析式为y=kx+t,并设P,Q的坐标分别为(xP,yP),(xQ,yQ).由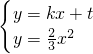 ,
,
得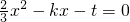 ,
,
于是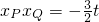 ,即
,即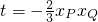 .
.
于是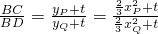 =
=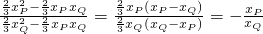 .,
.,
又因为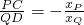 ,所以
,所以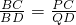 .
.
因为∠BCP=∠BDQ=90°,
所以△BCP∽△BDQ,
故∠ABP=∠ABQ;
(2)解:设PC=a,DQ=b,不妨设a≥b>0,由(1)可知
∠ABP=∠ABQ=30°,BC= ,BD=
,BD=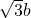 ,
,
所以AC=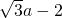 ,AD=
,AD=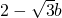 .
.
因为PC∥DQ,所以△ACP∽△ADQ.
于是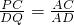 ,即
,即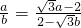 ,
,
所以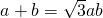 .
.
由(1)中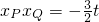 ,即
,即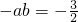 ,所以
,所以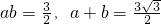 ,
,
于是可求得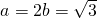 .
.
将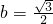 代入
代入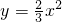 ,得到点Q的坐标(
,得到点Q的坐标( ,
, ).
).
再将点Q的坐标代入y=kx+1,求得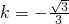 .
.
所以直线PQ的函数解析式为 .
.
根据对称性知,所求直线PQ的函数解析式为 或
或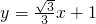 .
.
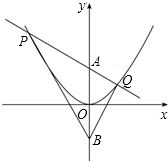
分析:(1)利用抛物线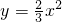 的图象上点的坐标特征,待定系数法球函数解析式,根与系数的关系和相似三角形的判定与性质解答即可;
的图象上点的坐标特征,待定系数法球函数解析式,根与系数的关系和相似三角形的判定与性质解答即可;
(2)利用(1)中已知与结论,继续由相似三角形,根与系数的关系、函数解析式求得结果.
点评:此题主要考查相似三角形的判定与性质、根与系数的关系、待定系数法求函数解析式以及对称解决问题.
设点A的坐标为(0,t),则点B的坐标为(0,-t).
设直线PQ的函数解析式为y=kx+t,并设P,Q的坐标分别为(xP,yP),(xQ,yQ).由
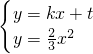 ,
,
得
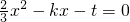 ,
,于是
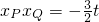 ,即
,即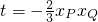 .
.于是
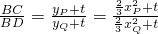 =
=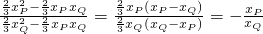 .,
.,又因为
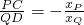 ,所以
,所以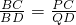 .
.因为∠BCP=∠BDQ=90°,
所以△BCP∽△BDQ,
故∠ABP=∠ABQ;
(2)解:设PC=a,DQ=b,不妨设a≥b>0,由(1)可知
∠ABP=∠ABQ=30°,BC=
 ,BD=
,BD=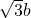 ,
,所以AC=
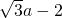 ,AD=
,AD=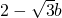 .
.因为PC∥DQ,所以△ACP∽△ADQ.
于是
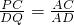 ,即
,即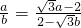 ,
,所以
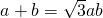 .
.由(1)中
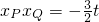 ,即
,即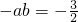 ,所以
,所以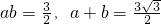 ,
,于是可求得
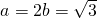 .
.将
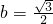 代入
代入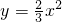 ,得到点Q的坐标(
,得到点Q的坐标( ,
, ).
).再将点Q的坐标代入y=kx+1,求得
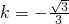 .
.所以直线PQ的函数解析式为
 .
.根据对称性知,所求直线PQ的函数解析式为
 或
或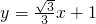 .
.分析:(1)利用抛物线
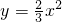 的图象上点的坐标特征,待定系数法球函数解析式,根与系数的关系和相似三角形的判定与性质解答即可;
的图象上点的坐标特征,待定系数法球函数解析式,根与系数的关系和相似三角形的判定与性质解答即可;(2)利用(1)中已知与结论,继续由相似三角形,根与系数的关系、函数解析式求得结果.
点评:此题主要考查相似三角形的判定与性质、根与系数的关系、待定系数法求函数解析式以及对称解决问题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 于P,Q两点.
于P,Q两点.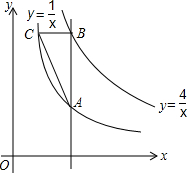 如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数
如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数 如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数y=
如图,点P为x轴正半轴上的一个点,过点P作x轴的垂线,交函数y=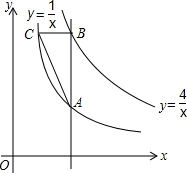 如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数
如图,点P为x轴正半轴上的一个点,过点P作x轴轴的垂线,交函数 的图象于点A,交函数
的图象于点A,交函数 的图象于点B,过点B作x轴的平行线,交
的图象于点B,过点B作x轴的平行线,交