题目内容
已知在平面直角坐标系中,过点P(0,2)任意作一条与抛物线y=ax2(a>0)交于两点的直线,设交点分别为A,B,若∠AOB=90°.
(1)判断A,B两点纵坐标的乘积是否为一个确定的值,并说明理由;
(2)确定抛物线y=ax2(a>0)的解析式.
解:(1)A,B两点纵坐标的乘积为一个确定的值,理由如下:
设直线AB的解析式为y=kx+2.
由 ,得ax2-kx-2=0 ③.
,得ax2-kx-2=0 ③.
设A(x1,y1),B(x2,y2),且x1<x2,
则x1,x2是方程③的两个实数根.
所以x1+x2= ,x1•x2=-
,x1•x2=- ,
,
 所以y1•y2=a
所以y1•y2=a •a
•a =a2•(x1•x2)2=a2•(-
=a2•(x1•x2)2=a2•(- )2=4;
)2=4;
所以A,B两点纵坐标的乘积为常数4,是一个确定的值;
(2)作AM⊥x轴于点M,BN⊥y轴于点N.
∵∠AOB=90°,
∴∠AOM+∠BON=90°,
∴∠AOM=∠OBN,
∴Rt△AOM∽Rt△OBN,
∴ =
= ,
,
∴ =
=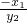 ,即-x1•x2=y1•y2,
,即-x1•x2=y1•y2,
∴-(- )=4,解得a=
)=4,解得a= .
.
所以抛物线的解析式为y= x2.
x2.
分析:(1)设过点P(0,2)的直线AB的解析式为y=kx+2,由 ,得ax2-kx-2=0③,再设A(x1,y1),B(x2,y2),且x1<x2,根据一元二次方程根与系数的关系,可知x1,x2是方程③的两个实数根,且x1+x2=
,得ax2-kx-2=0③,再设A(x1,y1),B(x2,y2),且x1<x2,根据一元二次方程根与系数的关系,可知x1,x2是方程③的两个实数根,且x1+x2= ,x1•x2=-
,x1•x2=- ,进而求出y1•y2=4,从而说明A,B两点纵坐标的乘积是一个确定的值;
,进而求出y1•y2=4,从而说明A,B两点纵坐标的乘积是一个确定的值;
(2)作AM⊥x轴于点M,BN⊥y轴于点N,先由∠AOB=90°,根据平角的定义得出∠AOM+∠BON=90°,由同角的余角相等得出∠AOM=∠OBN,根据两角对应相等的两三角形相似,证明Rt△AOM∽Rt△OBN,得到 =
= ,将A(x1,y1),B(x2,y2)两点的坐标代入,得出-x1•x2=y1•y2,即-(-
,将A(x1,y1),B(x2,y2)两点的坐标代入,得出-x1•x2=y1•y2,即-(- )=4,解方程求出a=
)=4,解方程求出a= ,从而得到抛物线的解析式.
,从而得到抛物线的解析式.
点评:本题考查了二次函数的综合题,其中涉及到运用待定系数法求二次函数的解析式,一元二次方程根与系数的关系,相似三角形的性质与判定等知识,综合性较强,有一定难度.
设直线AB的解析式为y=kx+2.
由
 ,得ax2-kx-2=0 ③.
,得ax2-kx-2=0 ③.设A(x1,y1),B(x2,y2),且x1<x2,
则x1,x2是方程③的两个实数根.
所以x1+x2=
 ,x1•x2=-
,x1•x2=- ,
, 所以y1•y2=a
所以y1•y2=a •a
•a =a2•(x1•x2)2=a2•(-
=a2•(x1•x2)2=a2•(- )2=4;
)2=4;所以A,B两点纵坐标的乘积为常数4,是一个确定的值;
(2)作AM⊥x轴于点M,BN⊥y轴于点N.
∵∠AOB=90°,
∴∠AOM+∠BON=90°,
∴∠AOM=∠OBN,
∴Rt△AOM∽Rt△OBN,
∴
 =
= ,
,∴
 =
=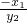 ,即-x1•x2=y1•y2,
,即-x1•x2=y1•y2,∴-(-
 )=4,解得a=
)=4,解得a= .
.所以抛物线的解析式为y=
 x2.
x2.分析:(1)设过点P(0,2)的直线AB的解析式为y=kx+2,由
 ,得ax2-kx-2=0③,再设A(x1,y1),B(x2,y2),且x1<x2,根据一元二次方程根与系数的关系,可知x1,x2是方程③的两个实数根,且x1+x2=
,得ax2-kx-2=0③,再设A(x1,y1),B(x2,y2),且x1<x2,根据一元二次方程根与系数的关系,可知x1,x2是方程③的两个实数根,且x1+x2= ,x1•x2=-
,x1•x2=- ,进而求出y1•y2=4,从而说明A,B两点纵坐标的乘积是一个确定的值;
,进而求出y1•y2=4,从而说明A,B两点纵坐标的乘积是一个确定的值;(2)作AM⊥x轴于点M,BN⊥y轴于点N,先由∠AOB=90°,根据平角的定义得出∠AOM+∠BON=90°,由同角的余角相等得出∠AOM=∠OBN,根据两角对应相等的两三角形相似,证明Rt△AOM∽Rt△OBN,得到
 =
= ,将A(x1,y1),B(x2,y2)两点的坐标代入,得出-x1•x2=y1•y2,即-(-
,将A(x1,y1),B(x2,y2)两点的坐标代入,得出-x1•x2=y1•y2,即-(- )=4,解方程求出a=
)=4,解方程求出a= ,从而得到抛物线的解析式.
,从而得到抛物线的解析式.点评:本题考查了二次函数的综合题,其中涉及到运用待定系数法求二次函数的解析式,一元二次方程根与系数的关系,相似三角形的性质与判定等知识,综合性较强,有一定难度.

练习册系列答案
相关题目
 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.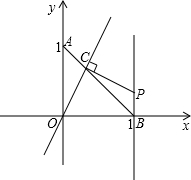 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.