Question

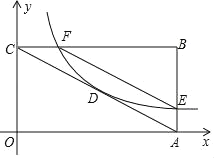
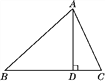
【题目】如图，△ABC的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD于E，交AB于F，交⊙O于G.

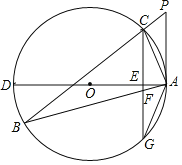
(1)判断直线PA与⊙O的位置关系，并说明理由；

(2)求证：AG2=AF·AB；

(3)求若⊙O的直径为10，AC=2，AB=4，求△AFG的面积.

Answer 1

【答案】（1）见解析；（2）见解析；（3）3.

【解析】

（1）首先连接CD，由AD为⊙O的直径，可得∠ACD=90°，然后由圆周角定理，证得∠B=∠D，由已知∠PAC=∠B，可证得DA⊥PA，继而可证得PA与⊙O相切．
（2）首先连接BG，易证得△AFG∽△AGB，然后由相似三角形的对应边成比例，证得结论；
（3）首先连接BD，由AG2=AFAB，可求得AF的长，易证得△AEF∽△ABD，即可求得AE的长，继而可求得EF与EG的长，则可求得答案．

（1）PA与⊙O相切．理由：
如图1，连接CD，
∵AD为⊙O的直径，
∴∠ACD=90°，
∴∠D+∠CAD=90°，A
∵∠B=∠D，∠PAC=∠B，
∴∠PAC=∠D，
∴∠PAC+∠CAD=90°，
即DA⊥PA，
∵点A在圆上，
∴PA与⊙O相切．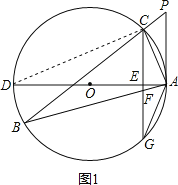

（2）

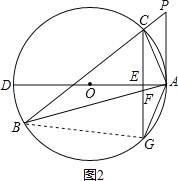
证明：如图2，连接BG，
∵AD为⊙O的直径，CG⊥AD，
∴ ，
∴∠AGF=∠ABG，
∵∠GAF=∠BAG，
∴△AGF∽△ABG，
∴AG：AB=AF：AG，
∴AG2=AFAB；

（3）

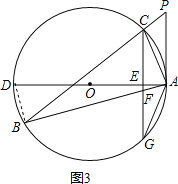
解：如图3，连接BD，
∵AD是直径，
∴∠ABD=90°，
∵AG2=AFAB，AG=AC=2 ，AB=4，
∴AF= =，
∵CG⊥AD，
∴∠AEF=∠ABD=90°，
∵∠EAF=∠BAD，
∴△AEF∽△ABD，
∴ ，
即，
解得：AE=2，
∴EF= =1，
∵EG==4，
∴FG=EG-EF=4-1=3，
∴S△AFG=FGAE=3×3×2=3．