题目内容
（2003•大连）如图，在离地面高度6米的C处引拉线固定电线杆，拉线和地面成61°角，求拉线AC的长以及拉线下端点A与杆底D的距离AD．（精确到0.01米）
【答案】分析：在直角△ACD中，已知锐角的度数，以及直角边CD的长，利用三角函数即可求得AC与AD的长．
解答：解：在直角△ACD中，∠ACD=90°-61°=29°．
∵tan∠ACD=
，
∴AD=CD•tan∠ACD=6×tan29°≈6×0.4848≈2.91米；
∵sin∠CAD=
，
∴AC=
≈
≈6.86米．
答：拉线AC的长是6.86米，拉线下端点A与杆底D的距离AD的长是2.91米．
点评：本题考查了利用三角函数求三角形的边长，正确理解三角函数的定义是关键．
解答：解：在直角△ACD中，∠ACD=90°-61°=29°．
∵tan∠ACD=
，∴AD=CD•tan∠ACD=6×tan29°≈6×0.4848≈2.91米；
∵sin∠CAD=
，∴AC=
≈≈6.86米．答：拉线AC的长是6.86米，拉线下端点A与杆底D的距离AD的长是2.91米．
点评：本题考查了利用三角函数求三角形的边长，正确理解三角函数的定义是关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
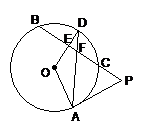（2003•大连）如图，PA是⊙O的切线，切点为A，PCB是⊙O的割线，交⊙O于C、B两点，半径OD⊥BC，垂足为E，AD交PB于点F，BF=PF．
，-
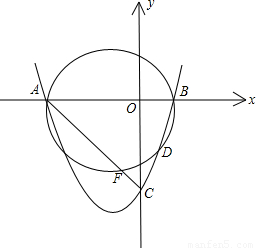
），B点坐标为（1，0）．
，-
），B点坐标为（1，0）．
