题目内容
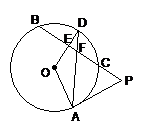 (2003•大连)如图,PA是⊙O的切线,切点为A,PCB是⊙O的割线,交⊙O于C、B两点,半径OD⊥BC,垂足为E,AD交PB于点F,BF=PF.
(2003•大连)如图,PA是⊙O的切线,切点为A,PCB是⊙O的割线,交⊙O于C、B两点,半径OD⊥BC,垂足为E,AD交PB于点F,BF=PF.(1)求证:PA=PF;
(2)若CF=1,切线PA的长为
2
2
.分析:(1)可通过证明角相等来得出边相等,本题中需要证明的相等角是∠PFA=∠PAF,我们看这两个角和哪些角有关系,∠PFA=∠DFE,∠D+∠DFE=∠D+∠DFA=90°,再看∠PAF,根据切线的性质可得出,∠PAF+∠OAD=90°,那么只要证明∠ODA=∠OAD,就能得出∠PFA=∠PAF的结论,而∠ODA=∠OAD正好可以用等边对等角来得出,因此便能证明出PA=PF;
(2)根据切割线定理我们可知:PA2=PC•PB,而PC=PF-1,PB=2PF,根据BF=PF=PA,那么将相等的线段进行置换即可求出PA的长.
(2)根据切割线定理我们可知:PA2=PC•PB,而PC=PF-1,PB=2PF,根据BF=PF=PA,那么将相等的线段进行置换即可求出PA的长.
解答:解:(1)证明:∵PA是圆O的切线,
∴∠OAD+∠PAF=90°…①,
∵OD=OA,
∴∠OAD=∠ODA…②,
∵OD⊥BC,
∴∠ODA+∠DFE=90°,而∠DFE=∠PFA,
∴∠PFA+∠ODA=90°…③,
根据①②③可得:∠PFA=∠PAF,
∴PA=PF;
(2)∵PA是圆O的切线,
∴PA2=PC•PB,
∵PC=PF-CF=PA-1,PB=2PF=2PA,
∴PA2=(PA-1)•2PA,
∴PA=2.
∴∠OAD+∠PAF=90°…①,
∵OD=OA,
∴∠OAD=∠ODA…②,
∵OD⊥BC,
∴∠ODA+∠DFE=90°,而∠DFE=∠PFA,
∴∠PFA+∠ODA=90°…③,
根据①②③可得:∠PFA=∠PAF,
∴PA=PF;
(2)∵PA是圆O的切线,
∴PA2=PC•PB,
∵PC=PF-CF=PA-1,PB=2PF=2PA,
∴PA2=(PA-1)•2PA,
∴PA=2.
点评:本题主要考查了切线的性质,切割线定理等知识点,根据切线的性质得出直角进而用等角的余角相等来求出边相等是解题的关键.

练习册系列答案
相关题目
 ,-
,- ),B点坐标为(1,0).
),B点坐标为(1,0).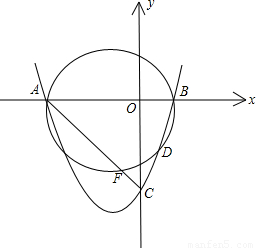
 ,-
,- ),B点坐标为(1,0).
),B点坐标为(1,0).